3. 1D Cartesian structured VDS along parallel lines

In this notebook, we perform pseudo-random variable density sampling along the phase encoding direction. A handcrafted density is designed and samples are then drawn by virtually inverting its cumulative density function. Then these samples define the selected phase encoding lines retained in the sampling mask. Low frequencies are more sampled than higher frequencies.

• Author: Philippe Ciuciu (philippe.ciuciu@cea.fr)

• Date: 06/24/2022

• Date : 04/02/2025 (use of BrainWeb database using multi-contrast T1/T2/etc imaging)

• Target: IEEE EMBS-SPS Summer School on Novel acquisition and image reconstruction strategies in accelerated Magnetic Resonance Imaging

#DISPLAY BRAIN PHANTOM
%matplotlib inline

import numpy as np
import os.path as op
import os
import math ; import cmath
import matplotlib.pyplot as plt
import sys

from skimage import data, io, filters

import pywt as pw
import matplotlib.pyplot as plt

import brainweb_dl as bwdl

plt.rcParams["image.origin"]="lower"
plt.rcParams["image.cmap"]='Greys_r'

mri_img = bwdl.get_mri(4, "T1")[70, ...].astype(np.float32)
#mri_img = bwdl.get_mri(4, "T2")[120, ...].astype(np.float32)
print(mri_img.shape)
img_size = mri_img.shape[0]
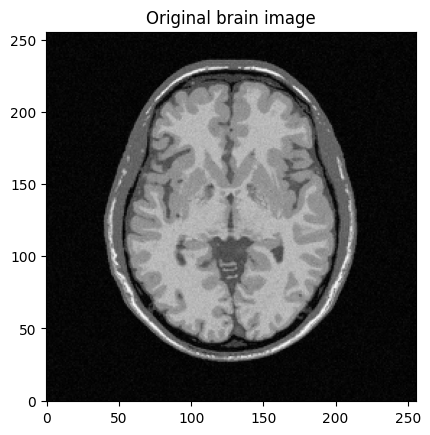
plt.figure()
plt.imshow(abs(mri_img))
plt.title("Original brain image")
plt.show()

/volatile/github-ci-mind-inria/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
  from .autonotebook import tqdm as notebook_tqdm

(256, 256)

import numpy as np
import sys
import numpy.random as ra

eps = sys.float_info.epsilon

c = np.ones((1, img_size), dtype="float64")
kspace_mask = np.tile(c, (img_size, 1))
#kspace_lines = np.linspace(-1/2., 1/2.,img_size)
kspace_lines = np.linspace(-1/2., 1/2.,img_size)*img_size
# define the taret sampling density (ie non-iniform over k-space lines)
decay = 1.
# Define the sampling density
p_decay = np.power(np.abs(kspace_lines),-decay)
p_decay = p_decay/np.sum(p_decay)
# generate its CDF
cdf_pdecay = np.cumsum(p_decay)


pmax = p_decay.max()
pmin = p_decay.min()

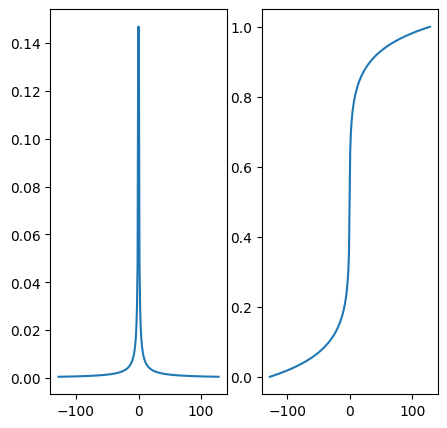
# Plot the density and its cumulative distribution function (CDF) p_decay
plt.figure()
fig, axs = plt.subplots(1, 2, figsize= (5,5) )
axs[0].plot(kspace_lines, p_decay)
axs[1].plot(kspace_lines, cdf_pdecay)

# Perform pseudo-random sampling: technique used:
# draw uniform variables and invert the CDF to get back to p_decay-distributed sampled
nb_samples = (int)(img_size/4)
print(nb_samples)
samples = ra.uniform(0, 1, nb_samples)
gen_klines = [int(kspace_lines[np.argwhere(cdf_pdecay == min(cdf_pdecay[(cdf_pdecay - r) > 0]))]) for r in samples]

# shift the samples lines by half of the k-space (ie image size as we're in Cartesian ref)
gen_klinesb = ((np.array(gen_klines) - 1) / 1).astype(int) + (int)(img_size/2)
#gen_klinesb = ((np.array(gen_klines) - 1) / 1).astype(int)
print(gen_klinesb)   # unsorted samples
times = np.arange(1, img_size, 1)
lc = np.bincount(gen_klinesb, minlength=len(times))

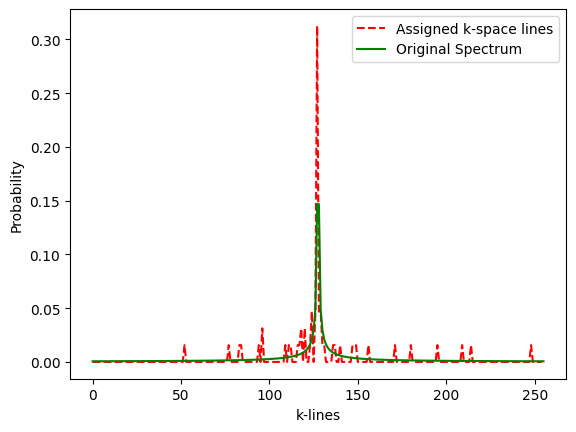
# check that histogram of sample values fits the prescribed density p_decay
plt.figure()
plot1, = plt.plot(lc/float(sum(lc)), 'r--', label='Assigned k-space lines')
plot2, = plt.plot(p_decay,'g',label='Original Spectrum')
plt.xlabel('k-lines')
plt.ylabel('Probability')
plt.legend(handles=[plot1,plot2])
plt.show()


#print(p_decay.min())
sampled_klines = np.array(np.unique(gen_klinesb))
print(sampled_klines)

nblines = np.size(sampled_klines)
print(nblines)
threshold = 2. * p_decay.min()  # sys.float_info.epsilon \simeq 2e-16
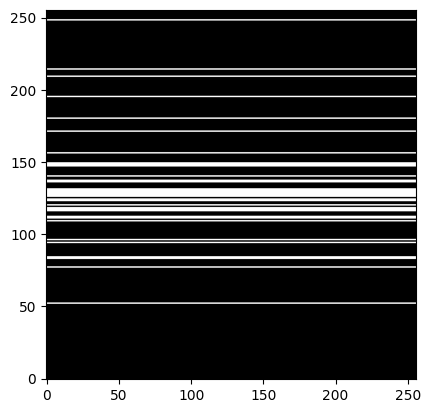
kspace_mask = np.zeros((img_size,img_size), dtype="float64")
kspace_mask[sampled_klines,:] = np.ones((nblines,img_size) , dtype="float64")

plt.figure()
plt.imshow(kspace_mask, cmap='gray')
plt.show()

64
[112  96  77 116 149 129 127 127 127 214 127 123 136  96 124 127 127 209
 118  94 128 127 126 127 129 117 195 127  83  84 137 127 127 118 140 180
 124 126 128 127 126 130 171 120 127 111 127 109  52 127 147 120 128 127
 129 127 156 127 131 248 148 127 127 124]

/tmp/ipykernel_1023388/2994268964.py:34: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
  gen_klines = [int(kspace_lines[np.argwhere(cdf_pdecay == min(cdf_pdecay[(cdf_pdecay - r) > 0]))]) for r in samples]

<Figure size 640x480 with 0 Axes>

[ 52  77  83  84  94  96 109 111 112 116 117 118 120 123 124 126 127 128
 129 130 131 136 137 140 147 148 149 156 171 180 195 209 214 248]
34

#import numpy.fft as fft
norm = "ortho"
#norm = None
def fft(x):
    return np.fft.fft2(x, norm=norm)

def ifft(x):
    return np.fft.ifft2(x, norm=norm)


# Generate the kspace data: first Fourier transform the image
kspace_data = np.fft.fftshift(fft(mri_img))
#add Gaussian complex-valued random noise
signoise = 10
#kspace_data += np.random.randn(*mri_img.shape) * signoise * (1+1j)
# Simulate independent noise realization on the real & imag parts
kspace_data += (np.random.randn(*mri_img.shape) + 1j * np.random.randn(*mri_img.shape)) * signoise

# Mask data to perform subsampling
kspace_data *= kspace_mask

# Zero order solution
image_rec0 = ifft(np.fft.ifftshift(kspace_data))

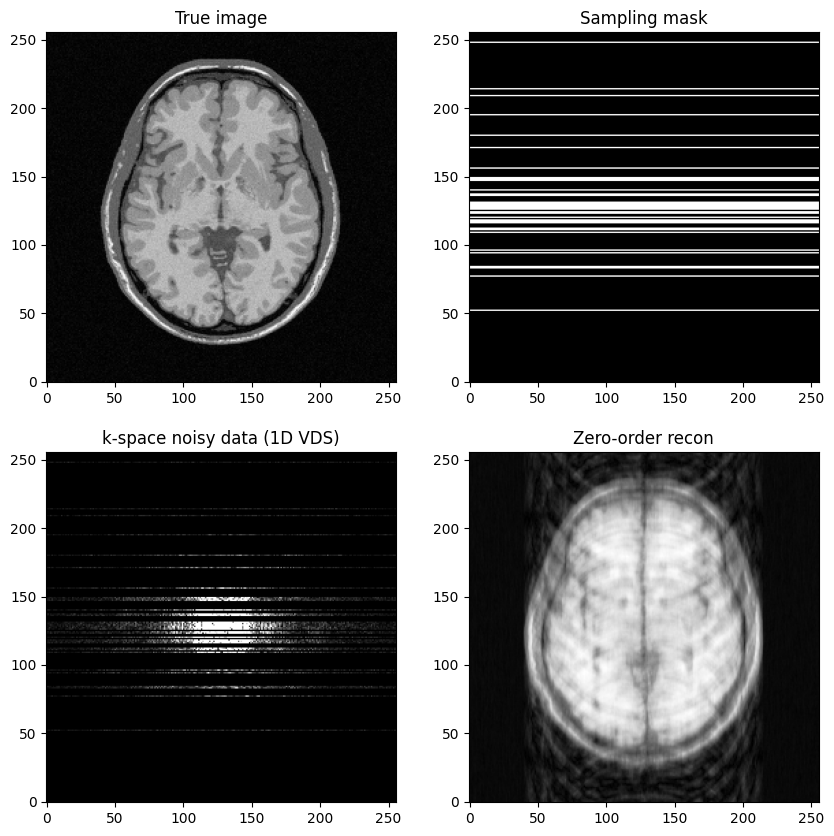
fig, axs = plt.subplots(2, 2, figsize=(10, 10) )
axs[0,0].imshow(mri_img, cmap='Greys_r')
axs[0,0].set_title("True image")
axs[0,1].imshow(kspace_mask, cmap='gray')
axs[0,1].set_title("Sampling mask")
axs[1,0].imshow(np.abs(kspace_data),  cmap='gray', vmax=0.005*np.abs(kspace_data).max())
#axs[1].imshow(np.abs(np.fft.ifftshift(kspace_data)), cmap='Greys_r')
axs[1,0].set_title("k-space noisy data (1D VDS)")
axs[1,1].imshow(np.abs(image_rec0), cmap='Greys_r')
axs[1,1].set_title("Zero-order recon")
plt.show()