12. Self-calibrated CS-pMR image reconstruction from undersampled non-Cartesian data#
In this tutorial we will reconstruct an MRI image from radial undersampled kspace measurements. Let us denote \(\Omega\) the undersampling mask, the under-sampled Fourier transform now reads \(F_{\Omega}\).
We use the toy datasets available in pysap, more specifically a 2D brain slice and under-sampled Cartesian acquisition over 32 channels. We compare zero-order image reconstruction with self-calibrated multi-coil Compressed sensing reconstructions (analysis vs synthesis formulation) using the FISTA algorithm for the synthesis formulation and the Condat-Vu algorithm for the analysis formulation. The multicoil data \((y_\ell)_\ell\) is collected across multiple, say \(L\), channels. The sensitivity maps \((S_\ell)_\ell\) are automically calibrated from the central portion of k-space (e.g. 5%) for all channels \(\ell=1, \ldots, L\).
We remind that the synthesis formulation of the non-Cartesian CS-PMRI problem reads (minimization in the sparsifying domain):
and the image solution is given by \(\widehat{x} = \Psi^*\widehat{z}\). For an orthonormal wavelet transform, we have \(n_\Psi=n\) while for a frame we may have \(n_\Psi > n\).
while the analysis formulation consists in minimizing the following cost function (min. in the image domain):
Author: Chaithya G R & Philippe Ciuciu
Date: 01/06/2021
Target: ATSI MSc students, Paris-Saclay University
# Package import
from mri.operators import NonCartesianFFT, WaveletN, WaveletUD2
from mri.operators.utils import convert_locations_to_mask, \
gridded_inverse_fourier_transform_nd
from mri.reconstructors import SelfCalibrationReconstructor
from mri.reconstructors.utils.extract_sensitivity_maps import get_Smaps
import pysap
from pysap.data import get_sample_data
# Third party import
from modopt.math.metrics import ssim
from modopt.opt.linear import Identity
from modopt.opt.proximity import SparseThreshold
import numpy as np
import matplotlib.pyplot as plt
/volatile/github-ci-mind-inria/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
Loading input data#
# Loading input data
cartesian_ref_image = get_sample_data('2d-pmri')
#image = pysap.Image(data=np.sqrt(np.sum(cartesian_ref_image.data**2, axis=0)))
image = np.linalg.norm(cartesian_ref_image, axis=0)
# Obtain MRI non-Cartesian radial mask
radial_mask = get_sample_data("mri-radial-samples")
kspace_loc = radial_mask.data
mask = pysap.Image(data=convert_locations_to_mask(kspace_loc, image.shape))
plt.subplot(1, 2, 1)
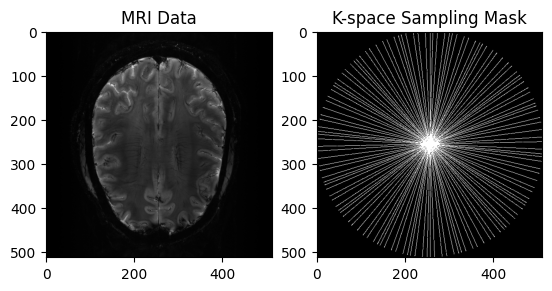
plt.imshow(np.abs(image), cmap='gray')
plt.title("MRI Data")
plt.subplot(1, 2, 2)
plt.imshow(mask, cmap='gray')
plt.title("K-space Sampling Mask")
plt.show()
Generate the kspace#
From the 2D brain slice and the acquisition mask, we retrospectively undersample the k-space using a non cartesian acquisition mask. We then grid the kspace to get the gridded solution as a baseline.
# Get the kspace observation values for the kspace locations
fourier_op = NonCartesianFFT(
samples=kspace_loc,
shape=image.shape,
n_coils=cartesian_ref_image.shape[0],
implementation='finufft' # Use gpuNUFFT for speed
)
kspace_obs = fourier_op.op(cartesian_ref_image.data)
/volatile/github-ci-mind-inria/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
Gridded solution
# Gridded solution
grid_space = np.linspace(-0.5, 0.5, num=image.shape[0])
grid2D = np.meshgrid(grid_space, grid_space)
grid_soln = np.asarray([
gridded_inverse_fourier_transform_nd(kspace_loc, kspace_obs_ch,
tuple(grid2D), 'linear')
for kspace_obs_ch in kspace_obs
])
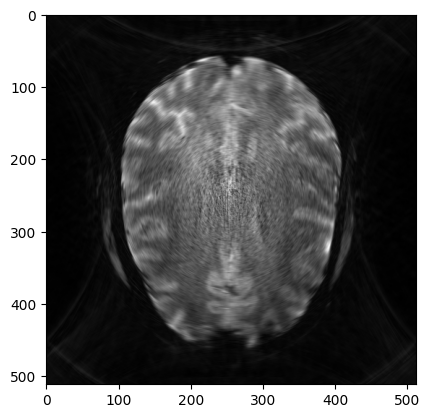
image_rec0 = pysap.Image(data=np.sqrt(np.sum(np.abs(grid_soln)**2, axis=0)))
plt.imshow(image_rec0, cmap='gray')
base_ssim = ssim(image_rec0, image)
print('The Base SSIM is : {}'.format(base_ssim))
The Base SSIM is : 0.6179867373261487
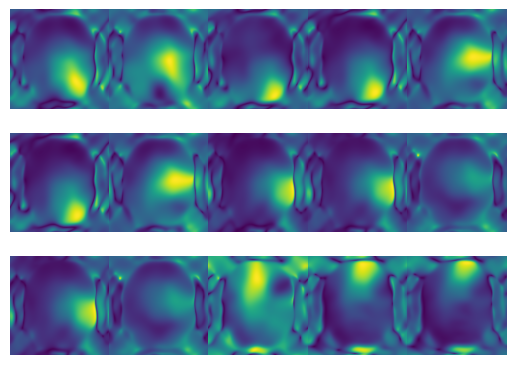
## Estimate Sensitivity maps (Smaps)
# Obtain SMaps
Smaps, SOS = get_Smaps(
k_space=kspace_obs,
img_shape=fourier_op.shape,
samples=kspace_loc,
thresh=(0.01, 0.01), # The cutoff threshold in each kspace direction
# between 0 and kspace_max (0.5)
min_samples=kspace_loc.min(axis=0),
max_samples=kspace_loc.max(axis=0),
mode='gridding',
method='linear',
n_cpu=-1,
)
h=3;w=5;
f, axs = plt.subplots(h,w)
for i in range(h):
for j in range(w):
axs[i, j].imshow(np.abs(Smaps[3 * i + j]))
axs[i, j].axis('off')
plt.subplots_adjust(wspace=0,hspace=0)
plt.show()
[Parallel(n_jobs=-1)]: Using backend LokyBackend with 48 concurrent workers.
[Parallel(n_jobs=-1)]: Done 3 out of 32 | elapsed: 4.3s remaining: 41.9s
[Parallel(n_jobs=-1)]: Done 32 out of 32 | elapsed: 5.5s finished
!pip install pynfft2
Collecting pynfft2
Using cached pyNFFT2-1.4.3-cp310-cp310-linux_x86_64.whl
Installing collected packages: pynfft2
Successfully installed pynfft2-1.4.3
[notice] A new release of pip is available: 23.0.1 -> 25.0.1
[notice] To update, run: pip install --upgrade pip
Setup Fourier operators with SENSE#
# Setup Fourier Operator with SENSE. This would initialize the
# fourier operators in the GPU.
# For this we need to specify the implementation as gpuNUFFT
# and also pass the Smaps calculated above
fourier_implementation = 'gpunufft'
fourier_op_sense = NonCartesianFFT(
samples=kspace_loc,
shape=image.shape,
n_coils=cartesian_ref_image.shape[0],
smaps=Smaps.astype(np.complex64),
implementation=fourier_implementation,
)
/volatile/github-ci-mind-inria/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mrinufft/operators/interfaces/gpunufft.py:146: UserWarning: no pinning provided, pinning existing smaps now.
warnings.warn("no pinning provided, pinning existing smaps now.")
FISTA optimization#
We now want to refine the zero order solution using a FISTA optimization. The cost function is set to Proximity Cost + Gradient Cost
# Setup the operators
linear_op = WaveletN(wavelet_name='sym8', nb_scale=4)
regularizer_op = SparseThreshold(Identity(), 1e-8, thresh_type="soft")
# Setup Reconstructor
reconstructor = SelfCalibrationReconstructor(
fourier_op=fourier_op_sense,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='synthesis',
lipschitz_cst=fourier_op_sense.impl.get_lipschitz_cst(),
verbose=1,
)
WARNING: Making input data immutable.
Lipschitz constant is 16.209678649902344
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[9], line 2
1 # Setup Reconstructor
----> 2 reconstructor = SelfCalibrationReconstructor(
3 fourier_op=fourier_op_sense,
4 linear_op=linear_op,
5 regularizer_op=regularizer_op,
6 gradient_formulation='synthesis',
7 lipschitz_cst=fourier_op_sense.impl.get_lipschitz_cst(),
8 verbose=1,
9 )
File ~/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mri/reconstructors/self_calibrating.py:151, in SelfCalibrationReconstructor.__init__(self, fourier_op, linear_op, gradient_formulation, kspace_portion, Smaps, smaps_extraction_mode, smaps_gridding_method, n_jobs, verbose, **kwargs)
149 self.n_jobs = n_jobs
150 if check_if_fourier_op_uses_sense(fourier_op):
--> 151 self.initialize_gradient_op(**self.extra_grad_args)
File ~/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mri/reconstructors/base.py:108, in ReconstructorBase.initialize_gradient_op(self, **extra_args)
106 def initialize_gradient_op(self, **extra_args):
107 # Initialize gradient operator and cost operators
--> 108 self.gradient_op = self.grad_class(
109 fourier_op=self.fourier_op,
110 verbose=self.verbose,
111 **extra_args,
112 )
File ~/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mri/operators/gradient/gradient.py:72, in GradSynthesis.__init__(self, fourier_op, linear_op, verbose, **kwargs)
69 coef = linear_op.op(np.squeeze(np.zeros((linear_op.n_coils,
70 *fourier_op.shape))))
71 self.linear_op_coeffs_shape = coef.shape
---> 72 super(GradSynthesis, self).__init__(
73 self._op_method,
74 self._trans_op_method,
75 self.linear_op_coeffs_shape,
76 verbose=verbose,
77 **kwargs,
78 )
File ~/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mri/operators/gradient/base.py:74, in GradBaseMRI.__init__(self, operator, trans_operator, shape, lips_calc_max_iter, lipschitz_cst, dtype, num_check_lips, verbose, **kwargs)
72 print("Lipschitz constant is " + str(self.spec_rad))
73 if num_check_lips > 0:
---> 74 is_lips = check_lipschitz_cst(f=self.trans_op_op,
75 x_shape=shape,
76 x_dtype=dtype,
77 lipschitz_cst=self.spec_rad,
78 max_nb_of_iter=num_check_lips)
79 if not is_lips:
80 raise ValueError('The lipschitz constraint is not satisfied')
File ~/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mri/operators/gradient/utils.py:48, in check_lipschitz_cst(f, x_shape, lipschitz_cst, max_nb_of_iter, x_dtype)
46 x = np.random.randn(*x_shape).astype(x_dtype)
47 y = np.random.randn(*x_shape).astype(x_dtype)
---> 48 is_lips_cst = (np.linalg.norm(f(x)-f(y)) <= (lipschitz_cst *
49 np.linalg.norm(x-y)))
51 return is_lips_cst
File ~/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/modopt/opt/gradient.py:202, in GradParent.trans_op_op(self, input_data)
176 def trans_op_op(self, input_data):
177 r"""Transpose Operation of the Operator.
178
179 This method calculates the action of the transpose operator on
(...)
200
201 """
--> 202 return self.trans_op(self.op(input_data))
File ~/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mri/operators/gradient/gradient.py:81, in GradSynthesis._op_method(self, data)
80 def _op_method(self, data):
---> 81 return self.fourier_op.op(self.linear_op.adj_op(data))
File ~/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mri/operators/fourier/non_cartesian.py:78, in NonCartesianFFT.op(self, data, *args)
65 def op(self, data, *args):
66 """Compute the masked non-uniform Fourier transform
67 of an image.
68
(...)
76 masked Fourier transform of the input image.
77 """
---> 78 return self.impl.op(data, *args)
File ~/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mrinufft/_array_compat.py:103, in with_numpy_cupy.<locals>.wrapper(*args, **kwargs)
100 xp = get_array_module(leading_arg)
102 # convert all to cupy / numpy according to data arg device
--> 103 args, kwargs = _to_numpy_cupy(args, kwargs, leading_arg)
105 # run function
106 ret_ = fun(*args, **kwargs)
File ~/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mrinufft/_array_compat.py:251, in _to_numpy_cupy(args, kwargs, leading_argument)
249 if is_cuda_array(leading_argument) and CUPY_AVAILABLE:
250 return _to_cupy(*args, **kwargs)
--> 251 elif is_cuda_tensor(leading_argument) and CUPY_AVAILABLE:
252 return _to_cupy(*args, **kwargs)
253 else:
File ~/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mrinufft/operators/interfaces/utils/gpu_utils.py:39, in is_cuda_tensor(var)
37 def is_cuda_tensor(var):
38 """Check if var is a CUDA tensor."""
---> 39 return isinstance(var, torch.Tensor) and var.is_cuda
NameError: name 'torch' is not defined
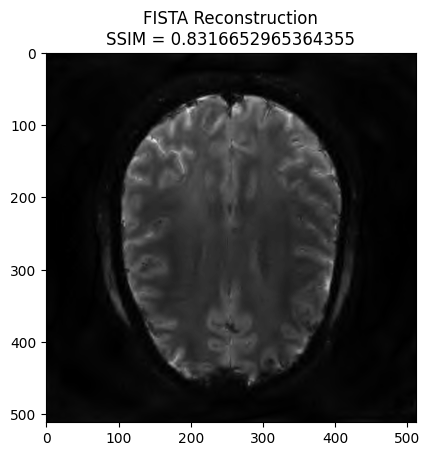
Synthesis formulation: FISTA optimization#
We now want to refine the zero order solution using a FISTA optimization. The cost function is set to Proximity Cost + Gradient Cost
x_final, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs.astype(np.complex64),
optimization_alg='fista',
num_iterations=100,
)
image_rec = pysap.Image(data=x_final)
recon_ssim = ssim(image_rec, image)
plt.imshow(np.abs(image_rec), cmap='gray')
plt.title('FISTA Reconstruction\nSSIM = {}'.format(recon_ssim))
plt.show()
- mu: 1e-08
- lipschitz constant: 16.209674835205078
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7e828675f7f0> - 4
- max iterations: 100
- image variable shape: (512, 512)
- alpha variable shape: (291721,)
----------------------------------------
Starting optimization...
WARNING: Making input data immutable.
- final iteration number: 100
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 8.400870646997646 seconds
----------------------------------------
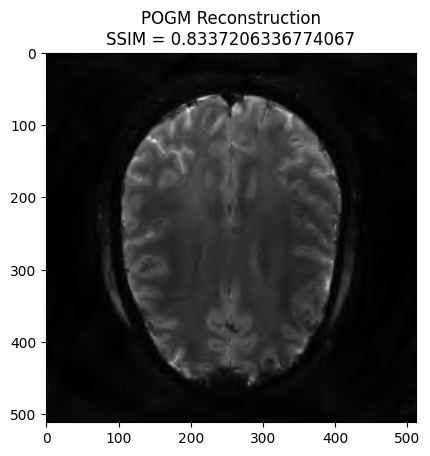
POGM reconstruction#
x_final, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='pogm',
num_iterations=200,
)
image_rec = pysap.Image(data=np.abs(x_final))
recon_ssim = ssim(image_rec, image)
plt.imshow(np.abs(image_rec), cmap='gray')
recon_ssim = ssim(image_rec, image)
plt.title('POGM Reconstruction\nSSIM = {}'.format(recon_ssim))
plt.show()
- mu: 1e-08
- lipschitz constant: 16.206116
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7e8282f94a00> - 4
- max iterations: 200
- image variable shape: (1, 512, 512)
----------------------------------------
Starting optimization...
- final iteration number: 200
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 530.4063913400023 seconds
----------------------------------------
Analysis formulation: Condat-Vu reconstruction#
#linear_op = WaveletN(wavelet_name="sym8", nb_scales=4)
linear_op = WaveletUD2(
wavelet_id=24,
nb_scale=4,
)
regularizer_op = SparseThreshold(Identity(), 1e-9, thresh_type="soft")
# Setup Reconstructor
reconstructor = SelfCalibrationReconstructor(
fourier_op=fourier_op_sense,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='analysis',
verbose=1,
)
WARNING: Making input data immutable.
Lipschitz constant is 11.98557472229004
x_final, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='condatvu',
num_iterations=200,
)
image_rec = pysap.Image(data=np.abs(x_final))
plt.imshow(np.abs(image_rec), cmap='gray')
recon_ssim = ssim(image_rec, image)
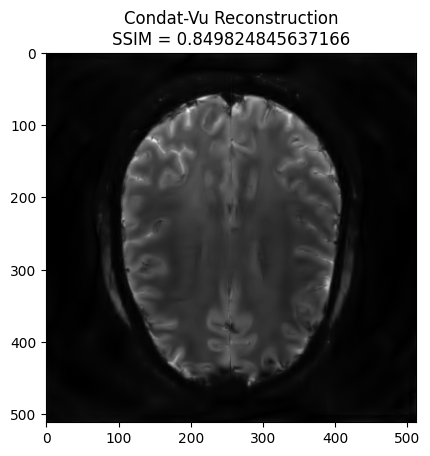
plt.title('Condat-Vu Reconstruction\nSSIM = {}'.format(recon_ssim))
plt.show()
- mu: 1e-09
- lipschitz constant: 11.98557472229004
- tau: 0.15362178825549028
- sigma: 0.5
- rho: 1.0
- std: None
- 1/tau - sigma||L||^2 >= beta/2: True
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletUD2 object at 0x7e8282e45090> - 4
- max iterations: 200
- number of reweights: 0
- primal variable shape: (512, 512)
- dual variable shape: (2621440,)
----------------------------------------
Starting optimization...
WARNING: <class 'mri.operators.linear.wavelet.WaveletUD2'> does not inherit an operator parent.
- final iteration number: 200
- final cost value: 1000000.0
- converged: False
Done.
Execution time: 707.4618570560051 seconds
----------------------------------------