10. Non-Cartesian MR image reconstruction#
In this tutorial we will reconstruct an MRI image from radial undersampled kspace measurements. Let us denote \(\Omega\) the undersampling mask, the under-sampled Fourier transform now reads \(F_{\Omega}\).
Import neuroimaging data#
We use the toy datasets available in pysap, more specifically a 2D brain slice and the radial under-sampling scheme. We compare zero-order image reconstruction with Compressed sensing reconstructions (analysis vs synthesis formulation) using the FISTA algorithm for the synthesis formulation and the Condat-Vu algorithm for the analysis formulation.
We remind that the synthesis formulation reads (minimization in the sparsifying domain):
and the image solution is given by \(\widehat{x} = \Psi^*\widehat{z}\). For an orthonormal wavelet transform, we have \(n_\Psi=n\) while for a frame we may have \(n_\Psi > n\).
while the analysis formulation consists in minimizing the following cost function (min. in the image domain):
Author: Chaithya G R & Philippe Ciuciu
Date: 01/06/2021
Target: ATSI MSc students, Paris-Saclay University
from mri.operators import NonCartesianFFT, WaveletUD2, WaveletN
from mri.operators.utils import convert_locations_to_mask, \
gridded_inverse_fourier_transform_nd
from mri.reconstructors import SingleChannelReconstructor
from pysap.data import get_sample_data
# Third party import
from modopt.math.metrics import ssim
from modopt.opt.linear import Identity
from modopt.opt.proximity import SparseThreshold
import numpy as np
import matplotlib.pyplot as plt
/volatile/github-ci-mind-inria/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
Loading input data#
image = get_sample_data('2d-mri').data.astype(np.complex64)
# Obtain MRI non-cartesian mask
radial_mask = get_sample_data("mri-radial-samples")
kspace_loc = radial_mask.data
View Input data#
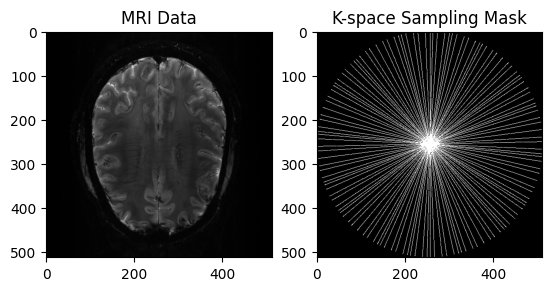
plt.subplot(1, 2, 1)
plt.imshow(np.abs(image), cmap='gray')
plt.title("MRI Data")
plt.subplot(1, 2, 2)
plt.imshow(convert_locations_to_mask(kspace_loc, image.shape), cmap='gray')
plt.title("K-space Sampling Mask")
plt.show()
Generate the kspace#
From the 2D brain slice and the acquisition mask, we retrospectively undersample the k-space using a radial mask. We then reconstruct the zero-order solution as a baseline
Get the locations of the kspace samples
# Get the locations of the kspace samples and the associated observations
#fourier_op = NonCartesianFFT(samples=kspace_loc, shape=image.shape, implementation='gpuNUFFT
#kspace_obs = fourier_op.op(image)[0]
fourier_op = NonCartesianFFT(samples=kspace_loc, shape=image.shape, implementation='finufft')
kspace_obs = fourier_op.op(image)
/volatile/github-ci-mind-inria/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
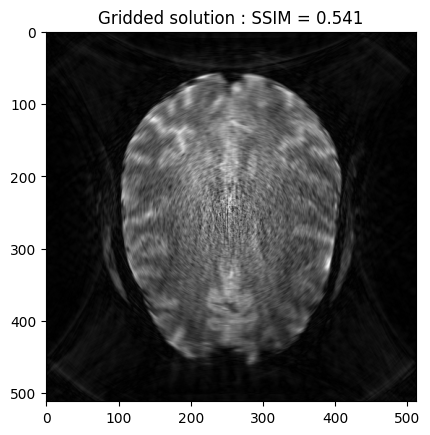
Gridded solution
grid_space = np.linspace(-0.5, 0.5, num=image.shape[0])
grid2D = np.meshgrid(grid_space, grid_space)
grid_soln = gridded_inverse_fourier_transform_nd(kspace_loc, kspace_obs,
tuple(grid2D), 'linear')
base_ssim = ssim(grid_soln, image)
plt.imshow(np.abs(grid_soln), cmap='gray')
plt.title('Gridded solution : SSIM = ' + str(np.around(base_ssim, 3)))
plt.show()
FISTA optimization#
We now want to refine the zero order solution using a FISTA optimization. The cost function is set to Proximity Cost + Gradient Cost
linear_op = WaveletN(wavelet_name="sym8", nb_scales=4)
regularizer_op = SparseThreshold(Identity(), 6 * 1e-7, thresh_type="soft")
Generate operators#
reconstructor = SingleChannelReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='synthesis',
verbose=1,
)
WARNING: Making input data immutable.
Lipschitz constant is 17.828468704223635
The lipschitz constraint is satisfied
Synthesis formulation: FISTA optimization#
We now want to refine the zero order solution using a FISTA optimization. The cost function is set to Proximity Cost + Gradient Cost
image_rec, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='fista',
num_iterations=200,
)
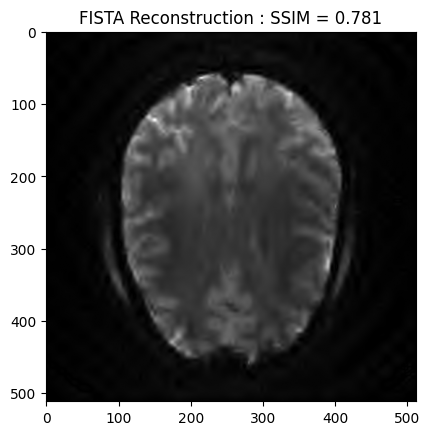
recon_ssim = ssim(image_rec, image)
plt.imshow(np.abs(image_rec), cmap='gray')
plt.title('FISTA Reconstruction : SSIM = ' + str(np.around(recon_ssim, 3)))
plt.show()
WARNING: Making input data immutable.
- mu: 6e-07
- lipschitz constant: 17.828468704223635
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x715257d592a0> - 4
- max iterations: 200
- image variable shape: (512, 512)
- alpha variable shape: (291721,)
----------------------------------------
Starting optimization...
0%| | 0/200 [00:00<?, ?it/s]
0%| | 1/200 [00:00<01:49, 1.82it/s]
1%| | 2/200 [00:01<01:49, 1.81it/s]
2%|▏ | 3/200 [00:01<01:49, 1.79it/s]
2%|▏ | 4/200 [00:02<01:49, 1.79it/s]
2%|▎ | 5/200 [00:02<01:48, 1.79it/s]
3%|▎ | 6/200 [00:03<01:47, 1.80it/s]
4%|▎ | 7/200 [00:03<01:47, 1.80it/s]
4%|▍ | 8/200 [00:04<01:46, 1.80it/s]
4%|▍ | 9/200 [00:05<01:46, 1.80it/s]
5%|▌ | 10/200 [00:05<01:46, 1.79it/s]
6%|▌ | 11/200 [00:06<01:47, 1.77it/s]
6%|▌ | 12/200 [00:06<01:45, 1.77it/s]
6%|▋ | 13/200 [00:07<01:45, 1.77it/s]
7%|▋ | 14/200 [00:07<01:44, 1.79it/s]
8%|▊ | 15/200 [00:08<01:35, 1.95it/s]
8%|▊ | 16/200 [00:08<01:37, 1.90it/s]
8%|▊ | 17/200 [00:09<01:27, 2.08it/s]
9%|▉ | 18/200 [00:09<01:13, 2.48it/s]
10%|▉ | 19/200 [00:09<01:21, 2.22it/s]
10%|█ | 20/200 [00:10<01:27, 2.07it/s]
10%|█ | 21/200 [00:11<01:30, 1.98it/s]
11%|█ | 22/200 [00:11<01:32, 1.93it/s]
12%|█▏ | 23/200 [00:12<01:34, 1.87it/s]
12%|█▏ | 24/200 [00:12<01:35, 1.85it/s]
12%|█▎ | 25/200 [00:13<01:35, 1.84it/s]
13%|█▎ | 26/200 [00:13<01:35, 1.83it/s]
14%|█▎ | 27/200 [00:14<01:35, 1.82it/s]
14%|█▍ | 28/200 [00:14<01:35, 1.81it/s]
14%|█▍ | 29/200 [00:15<01:34, 1.81it/s]
15%|█▌ | 30/200 [00:16<01:35, 1.79it/s]
16%|█▌ | 31/200 [00:16<01:24, 2.01it/s]
16%|█▌ | 32/200 [00:17<01:26, 1.94it/s]
16%|█▋ | 33/200 [00:17<01:27, 1.90it/s]
17%|█▋ | 34/200 [00:18<01:28, 1.87it/s]
18%|█▊ | 35/200 [00:18<01:28, 1.86it/s]
18%|█▊ | 36/200 [00:19<01:29, 1.84it/s]
18%|█▊ | 37/200 [00:19<01:29, 1.83it/s]
19%|█▉ | 38/200 [00:20<01:29, 1.81it/s]
20%|█▉ | 39/200 [00:20<01:15, 2.14it/s]
20%|██ | 40/200 [00:20<01:04, 2.49it/s]
20%|██ | 41/200 [00:21<00:55, 2.84it/s]
21%|██ | 42/200 [00:21<00:50, 3.11it/s]
22%|██▏ | 43/200 [00:21<00:49, 3.19it/s]
22%|██▏ | 44/200 [00:22<00:52, 2.94it/s]
22%|██▎ | 45/200 [00:22<01:03, 2.45it/s]
23%|██▎ | 46/200 [00:23<01:09, 2.21it/s]
24%|██▎ | 47/200 [00:23<01:07, 2.28it/s]
24%|██▍ | 48/200 [00:24<01:11, 2.12it/s]
24%|██▍ | 49/200 [00:24<01:15, 2.01it/s]
25%|██▌ | 50/200 [00:25<01:17, 1.94it/s]
26%|██▌ | 51/200 [00:25<01:18, 1.89it/s]
26%|██▌ | 52/200 [00:26<01:19, 1.85it/s]
26%|██▋ | 53/200 [00:26<01:20, 1.83it/s]
27%|██▋ | 54/200 [00:27<01:19, 1.83it/s]
28%|██▊ | 55/200 [00:28<01:19, 1.82it/s]
28%|██▊ | 56/200 [00:28<01:19, 1.80it/s]
28%|██▊ | 57/200 [00:29<01:20, 1.79it/s]
29%|██▉ | 58/200 [00:29<01:20, 1.77it/s]
30%|██▉ | 59/200 [00:30<01:19, 1.77it/s]
30%|███ | 60/200 [00:30<01:19, 1.77it/s]
30%|███ | 61/200 [00:31<01:18, 1.77it/s]
31%|███ | 62/200 [00:31<01:18, 1.77it/s]
32%|███▏ | 63/200 [00:32<01:17, 1.76it/s]
32%|███▏ | 64/200 [00:33<01:17, 1.76it/s]
32%|███▎ | 65/200 [00:33<01:16, 1.77it/s]
33%|███▎ | 66/200 [00:34<01:16, 1.75it/s]
34%|███▎ | 67/200 [00:34<01:16, 1.74it/s]
34%|███▍ | 68/200 [00:35<01:15, 1.75it/s]
34%|███▍ | 69/200 [00:35<01:14, 1.75it/s]
35%|███▌ | 70/200 [00:36<01:14, 1.75it/s]
36%|███▌ | 71/200 [00:37<01:13, 1.76it/s]
36%|███▌ | 72/200 [00:37<01:12, 1.76it/s]
36%|███▋ | 73/200 [00:38<01:12, 1.76it/s]
37%|███▋ | 74/200 [00:38<01:11, 1.77it/s]
38%|███▊ | 75/200 [00:39<01:10, 1.77it/s]
38%|███▊ | 76/200 [00:39<01:10, 1.77it/s]
38%|███▊ | 77/200 [00:40<01:09, 1.77it/s]
39%|███▉ | 78/200 [00:41<01:08, 1.78it/s]
40%|███▉ | 79/200 [00:41<01:08, 1.76it/s]
40%|████ | 80/200 [00:42<01:08, 1.75it/s]
40%|████ | 81/200 [00:42<01:07, 1.76it/s]
41%|████ | 82/200 [00:43<01:06, 1.78it/s]
42%|████▏ | 83/200 [00:43<01:06, 1.76it/s]
42%|████▏ | 84/200 [00:44<01:06, 1.75it/s]
42%|████▎ | 85/200 [00:45<01:05, 1.77it/s]
43%|████▎ | 86/200 [00:45<01:04, 1.76it/s]
44%|████▎ | 87/200 [00:46<01:04, 1.75it/s]
44%|████▍ | 88/200 [00:46<01:03, 1.77it/s]
44%|████▍ | 89/200 [00:47<01:02, 1.77it/s]
45%|████▌ | 90/200 [00:47<01:02, 1.77it/s]
46%|████▌ | 91/200 [00:48<01:01, 1.77it/s]
46%|████▌ | 92/200 [00:49<01:01, 1.77it/s]
46%|████▋ | 93/200 [00:49<01:00, 1.76it/s]
47%|████▋ | 94/200 [00:50<01:00, 1.76it/s]
48%|████▊ | 95/200 [00:50<00:59, 1.76it/s]
48%|████▊ | 96/200 [00:51<00:58, 1.77it/s]
48%|████▊ | 97/200 [00:51<00:57, 1.79it/s]
49%|████▉ | 98/200 [00:52<00:57, 1.79it/s]
50%|████▉ | 99/200 [00:52<00:56, 1.79it/s]
50%|█████ | 100/200 [00:53<00:55, 1.79it/s]
50%|█████ | 101/200 [00:54<00:55, 1.79it/s]
51%|█████ | 102/200 [00:54<00:54, 1.80it/s]
52%|█████▏ | 103/200 [00:55<00:53, 1.81it/s]
52%|█████▏ | 104/200 [00:55<00:53, 1.80it/s]
52%|█████▎ | 105/200 [00:56<00:52, 1.80it/s]
53%|█████▎ | 106/200 [00:56<00:51, 1.81it/s]
54%|█████▎ | 107/200 [00:57<00:52, 1.78it/s]
54%|█████▍ | 108/200 [00:57<00:51, 1.78it/s]
55%|█████▍ | 109/200 [00:58<00:50, 1.80it/s]
55%|█████▌ | 110/200 [00:59<00:50, 1.78it/s]
56%|█████▌ | 111/200 [00:59<00:42, 2.10it/s]
56%|█████▌ | 112/200 [00:59<00:36, 2.41it/s]
56%|█████▋ | 113/200 [00:59<00:32, 2.67it/s]
57%|█████▋ | 114/200 [01:00<00:28, 3.02it/s]
57%|█████▊ | 115/200 [01:00<00:26, 3.21it/s]
58%|█████▊ | 116/200 [01:00<00:24, 3.41it/s]
58%|█████▊ | 117/200 [01:00<00:23, 3.52it/s]
59%|█████▉ | 118/200 [01:01<00:23, 3.49it/s]
60%|█████▉ | 119/200 [01:01<00:22, 3.54it/s]
60%|██████ | 120/200 [01:02<00:29, 2.72it/s]
60%|██████ | 121/200 [01:02<00:33, 2.35it/s]
61%|██████ | 122/200 [01:03<00:36, 2.13it/s]
62%|██████▏ | 123/200 [01:03<00:33, 2.28it/s]
62%|██████▏ | 124/200 [01:04<00:36, 2.10it/s]
62%|██████▎ | 125/200 [01:04<00:37, 1.99it/s]
63%|██████▎ | 126/200 [01:05<00:38, 1.92it/s]
64%|██████▎ | 127/200 [01:05<00:38, 1.88it/s]
64%|██████▍ | 128/200 [01:06<00:39, 1.83it/s]
64%|██████▍ | 129/200 [01:06<00:39, 1.81it/s]
65%|██████▌ | 130/200 [01:07<00:38, 1.80it/s]
66%|██████▌ | 131/200 [01:07<00:35, 1.96it/s]
66%|██████▌ | 132/200 [01:08<00:35, 1.91it/s]
66%|██████▋ | 133/200 [01:09<00:35, 1.86it/s]
67%|██████▋ | 134/200 [01:09<00:35, 1.83it/s]
68%|██████▊ | 135/200 [01:10<00:35, 1.82it/s]
68%|██████▊ | 136/200 [01:10<00:35, 1.79it/s]
68%|██████▊ | 137/200 [01:11<00:35, 1.79it/s]
69%|██████▉ | 138/200 [01:11<00:34, 1.80it/s]
70%|██████▉ | 139/200 [01:12<00:33, 1.80it/s]
70%|███████ | 140/200 [01:12<00:33, 1.79it/s]
70%|███████ | 141/200 [01:13<00:33, 1.78it/s]
71%|███████ | 142/200 [01:14<00:32, 1.77it/s]
72%|███████▏ | 143/200 [01:14<00:32, 1.77it/s]
72%|███████▏ | 144/200 [01:15<00:28, 1.95it/s]
72%|███████▎ | 145/200 [01:15<00:29, 1.88it/s]
73%|███████▎ | 146/200 [01:16<00:29, 1.84it/s]
74%|███████▎ | 147/200 [01:16<00:29, 1.81it/s]
74%|███████▍ | 148/200 [01:17<00:29, 1.79it/s]
74%|███████▍ | 149/200 [01:17<00:28, 1.79it/s]
75%|███████▌ | 150/200 [01:18<00:27, 1.79it/s]
76%|███████▌ | 151/200 [01:19<00:27, 1.79it/s]
76%|███████▌ | 152/200 [01:19<00:26, 1.78it/s]
76%|███████▋ | 153/200 [01:20<00:26, 1.77it/s]
77%|███████▋ | 154/200 [01:20<00:25, 1.77it/s]
78%|███████▊ | 155/200 [01:21<00:25, 1.76it/s]
78%|███████▊ | 156/200 [01:21<00:24, 1.76it/s]
78%|███████▊ | 157/200 [01:22<00:24, 1.75it/s]
79%|███████▉ | 158/200 [01:23<00:24, 1.75it/s]
80%|███████▉ | 159/200 [01:23<00:23, 1.75it/s]
80%|████████ | 160/200 [01:24<00:22, 1.76it/s]
80%|████████ | 161/200 [01:24<00:22, 1.76it/s]
81%|████████ | 162/200 [01:25<00:21, 1.76it/s]
82%|████████▏ | 163/200 [01:25<00:21, 1.76it/s]
82%|████████▏ | 164/200 [01:26<00:20, 1.77it/s]
82%|████████▎ | 165/200 [01:26<00:19, 1.78it/s]
83%|████████▎ | 166/200 [01:27<00:19, 1.78it/s]
84%|████████▎ | 167/200 [01:28<00:18, 1.79it/s]
84%|████████▍ | 168/200 [01:28<00:17, 1.79it/s]
84%|████████▍ | 169/200 [01:29<00:17, 1.78it/s]
85%|████████▌ | 170/200 [01:29<00:16, 1.79it/s]
86%|████████▌ | 171/200 [01:30<00:16, 1.79it/s]
86%|████████▌ | 172/200 [01:30<00:15, 1.79it/s]
86%|████████▋ | 173/200 [01:31<00:15, 1.80it/s]
87%|████████▋ | 174/200 [01:31<00:14, 1.81it/s]
88%|████████▊ | 175/200 [01:32<00:13, 1.80it/s]
88%|████████▊ | 176/200 [01:33<00:13, 1.80it/s]
88%|████████▊ | 177/200 [01:33<00:12, 1.80it/s]
89%|████████▉ | 178/200 [01:34<00:12, 1.80it/s]
90%|████████▉ | 179/200 [01:34<00:11, 1.81it/s]
90%|█████████ | 180/200 [01:35<00:11, 1.80it/s]
90%|█████████ | 181/200 [01:35<00:10, 1.79it/s]
91%|█████████ | 182/200 [01:36<00:10, 1.80it/s]
92%|█████████▏| 183/200 [01:36<00:09, 1.81it/s]
92%|█████████▏| 184/200 [01:37<00:08, 1.79it/s]
92%|█████████▎| 185/200 [01:38<00:08, 1.79it/s]
93%|█████████▎| 186/200 [01:38<00:07, 1.80it/s]
94%|█████████▎| 187/200 [01:39<00:07, 1.81it/s]
94%|█████████▍| 188/200 [01:39<00:06, 1.79it/s]
94%|█████████▍| 189/200 [01:40<00:05, 2.01it/s]
95%|█████████▌| 190/200 [01:40<00:04, 2.30it/s]
96%|█████████▌| 191/200 [01:40<00:03, 2.70it/s]
96%|█████████▌| 192/200 [01:40<00:02, 2.97it/s]
96%|█████████▋| 193/200 [01:41<00:02, 2.77it/s]
97%|█████████▋| 194/200 [01:41<00:02, 2.36it/s]
98%|█████████▊| 195/200 [01:42<00:02, 2.37it/s]
98%|█████████▊| 196/200 [01:42<00:01, 2.16it/s]
98%|█████████▊| 197/200 [01:43<00:01, 2.02it/s]
99%|█████████▉| 198/200 [01:43<00:01, 1.95it/s]
100%|█████████▉| 199/200 [01:44<00:00, 1.92it/s]
100%|██████████| 200/200 [01:45<00:00, 1.87it/s]
100%|██████████| 200/200 [01:45<00:00, 1.90it/s]
- final iteration number: 200
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 105.1125933593139 seconds
----------------------------------------
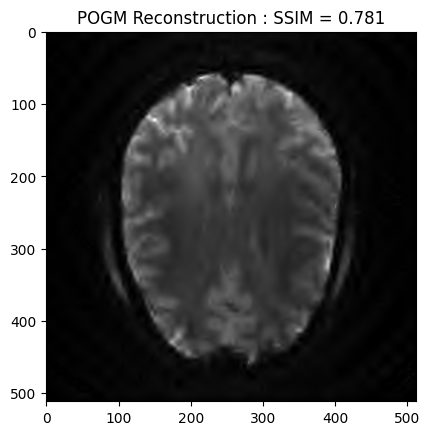
POGM reconstruction#
image_rec2, costs2, metrics2 = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='pogm',
num_iterations=200,
)
recon2_ssim = ssim(image_rec2, image)
plt.imshow(np.abs(image_rec2), cmap='gray')
plt.title('POGM Reconstruction : SSIM = ' + str(np.around(recon2_ssim, 3)))
plt.show()
- mu: 6e-07
- lipschitz constant: 17.828468704223635
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x715257d592a0> - 4
- max iterations: 200
- image variable shape: (1, 512, 512)
----------------------------------------
Starting optimization...
0%| | 0/200 [00:00<?, ?it/s]
0%| | 1/200 [00:00<01:22, 2.41it/s]
1%| | 2/200 [00:01<01:42, 1.93it/s]
2%|▏ | 3/200 [00:01<01:48, 1.82it/s]
2%|▏ | 4/200 [00:02<01:46, 1.84it/s]
2%|▎ | 5/200 [00:02<01:47, 1.81it/s]
3%|▎ | 6/200 [00:03<01:49, 1.77it/s]
4%|▎ | 7/200 [00:03<01:50, 1.74it/s]
4%|▍ | 8/200 [00:04<01:49, 1.76it/s]
4%|▍ | 9/200 [00:04<01:47, 1.77it/s]
5%|▌ | 10/200 [00:05<01:48, 1.75it/s]
6%|▌ | 11/200 [00:06<01:47, 1.75it/s]
6%|▌ | 12/200 [00:06<01:47, 1.75it/s]
6%|▋ | 13/200 [00:07<01:47, 1.74it/s]
7%|▋ | 14/200 [00:07<01:46, 1.75it/s]
8%|▊ | 15/200 [00:08<01:46, 1.74it/s]
8%|▊ | 16/200 [00:08<01:36, 1.90it/s]
8%|▊ | 17/200 [00:09<01:19, 2.31it/s]
9%|▉ | 18/200 [00:09<01:27, 2.09it/s]
10%|▉ | 19/200 [00:10<01:31, 1.98it/s]
10%|█ | 20/200 [00:10<01:34, 1.91it/s]
10%|█ | 21/200 [00:11<01:36, 1.86it/s]
11%|█ | 22/200 [00:11<01:36, 1.84it/s]
12%|█▏ | 23/200 [00:12<01:38, 1.81it/s]
12%|█▏ | 24/200 [00:13<01:39, 1.77it/s]
12%|█▎ | 25/200 [00:13<01:29, 1.96it/s]
13%|█▎ | 26/200 [00:14<01:31, 1.91it/s]
14%|█▎ | 27/200 [00:14<01:32, 1.87it/s]
14%|█▍ | 28/200 [00:14<01:24, 2.03it/s]
14%|█▍ | 29/200 [00:15<01:27, 1.95it/s]
15%|█▌ | 30/200 [00:16<01:30, 1.88it/s]
16%|█▌ | 31/200 [00:16<01:32, 1.83it/s]
16%|█▌ | 32/200 [00:17<01:32, 1.81it/s]
16%|█▋ | 33/200 [00:17<01:33, 1.79it/s]
17%|█▋ | 34/200 [00:18<01:33, 1.78it/s]
18%|█▊ | 35/200 [00:18<01:32, 1.78it/s]
18%|█▊ | 36/200 [00:19<01:33, 1.76it/s]
18%|█▊ | 37/200 [00:20<01:32, 1.77it/s]
19%|█▉ | 38/200 [00:20<01:31, 1.78it/s]
20%|█▉ | 39/200 [00:21<01:31, 1.76it/s]
20%|██ | 40/200 [00:21<01:30, 1.76it/s]
20%|██ | 41/200 [00:22<01:29, 1.77it/s]
21%|██ | 42/200 [00:22<01:29, 1.76it/s]
22%|██▏ | 43/200 [00:23<01:29, 1.75it/s]
22%|██▏ | 44/200 [00:24<01:29, 1.74it/s]
22%|██▎ | 45/200 [00:24<01:28, 1.75it/s]
23%|██▎ | 46/200 [00:25<01:19, 1.94it/s]
24%|██▎ | 47/200 [00:25<01:21, 1.87it/s]
24%|██▍ | 48/200 [00:26<01:22, 1.84it/s]
24%|██▍ | 49/200 [00:26<01:23, 1.81it/s]
25%|██▌ | 50/200 [00:27<01:23, 1.80it/s]
26%|██▌ | 51/200 [00:27<01:23, 1.77it/s]
26%|██▌ | 52/200 [00:28<01:23, 1.77it/s]
26%|██▋ | 53/200 [00:29<01:23, 1.77it/s]
27%|██▋ | 54/200 [00:29<01:22, 1.77it/s]
28%|██▊ | 55/200 [00:30<01:14, 1.95it/s]
28%|██▊ | 56/200 [00:30<01:16, 1.89it/s]
28%|██▊ | 57/200 [00:31<01:18, 1.82it/s]
29%|██▉ | 58/200 [00:31<01:19, 1.79it/s]
30%|██▉ | 59/200 [00:32<01:19, 1.77it/s]
30%|███ | 60/200 [00:32<01:18, 1.78it/s]
30%|███ | 61/200 [00:33<01:17, 1.79it/s]
31%|███ | 62/200 [00:33<01:08, 2.02it/s]
32%|███▏ | 63/200 [00:34<01:00, 2.27it/s]
32%|███▏ | 64/200 [00:34<00:59, 2.29it/s]
32%|███▎ | 65/200 [00:35<01:01, 2.18it/s]
33%|███▎ | 66/200 [00:35<00:53, 2.51it/s]
34%|███▎ | 67/200 [00:35<00:45, 2.91it/s]
34%|███▍ | 68/200 [00:35<00:40, 3.23it/s]
34%|███▍ | 69/200 [00:36<00:45, 2.87it/s]
35%|███▌ | 70/200 [00:36<00:53, 2.42it/s]
36%|███▌ | 71/200 [00:37<00:59, 2.18it/s]
36%|███▌ | 72/200 [00:37<01:02, 2.04it/s]
36%|███▋ | 73/200 [00:38<01:05, 1.94it/s]
37%|███▋ | 74/200 [00:39<01:07, 1.87it/s]
38%|███▊ | 75/200 [00:39<01:07, 1.86it/s]
38%|███▊ | 76/200 [00:40<01:07, 1.84it/s]
38%|███▊ | 77/200 [00:40<01:07, 1.81it/s]
39%|███▉ | 78/200 [00:41<01:07, 1.80it/s]
40%|███▉ | 79/200 [00:41<01:08, 1.78it/s]
40%|████ | 80/200 [00:42<01:07, 1.77it/s]
40%|████ | 81/200 [00:42<01:07, 1.77it/s]
41%|████ | 82/200 [00:43<01:06, 1.77it/s]
42%|████▏ | 83/200 [00:44<01:05, 1.77it/s]
42%|████▏ | 84/200 [00:44<01:05, 1.77it/s]
42%|████▎ | 85/200 [00:45<01:06, 1.73it/s]
43%|████▎ | 86/200 [00:45<01:05, 1.73it/s]
44%|████▎ | 87/200 [00:46<01:05, 1.73it/s]
44%|████▍ | 88/200 [00:47<01:04, 1.74it/s]
44%|████▍ | 89/200 [00:47<01:03, 1.74it/s]
45%|████▌ | 90/200 [00:48<01:03, 1.74it/s]
46%|████▌ | 91/200 [00:48<01:02, 1.75it/s]
46%|████▌ | 92/200 [00:49<01:01, 1.77it/s]
46%|████▋ | 93/200 [00:49<01:00, 1.76it/s]
47%|████▋ | 94/200 [00:50<00:59, 1.77it/s]
48%|████▊ | 95/200 [00:50<00:59, 1.77it/s]
48%|████▊ | 96/200 [00:51<00:58, 1.78it/s]
48%|████▊ | 97/200 [00:52<00:58, 1.75it/s]
49%|████▉ | 98/200 [00:52<00:58, 1.75it/s]
50%|████▉ | 99/200 [00:53<00:57, 1.76it/s]
50%|█████ | 100/200 [00:53<00:52, 1.92it/s]
50%|█████ | 101/200 [00:54<00:47, 2.09it/s]
51%|█████ | 102/200 [00:54<00:49, 1.98it/s]
52%|█████▏ | 103/200 [00:55<00:50, 1.91it/s]
52%|█████▏ | 104/200 [00:55<00:51, 1.86it/s]
52%|█████▎ | 105/200 [00:56<00:52, 1.80it/s]
53%|█████▎ | 106/200 [00:56<00:52, 1.78it/s]
54%|█████▎ | 107/200 [00:57<00:53, 1.74it/s]
54%|█████▍ | 108/200 [00:58<00:53, 1.73it/s]
55%|█████▍ | 109/200 [00:58<00:48, 1.87it/s]
55%|█████▌ | 110/200 [00:59<00:48, 1.84it/s]
56%|█████▌ | 111/200 [00:59<00:48, 1.83it/s]
56%|█████▌ | 112/200 [01:00<00:48, 1.80it/s]
56%|█████▋ | 113/200 [01:00<00:48, 1.80it/s]
57%|█████▋ | 114/200 [01:01<00:48, 1.78it/s]
57%|█████▊ | 115/200 [01:01<00:48, 1.76it/s]
58%|█████▊ | 116/200 [01:02<00:48, 1.75it/s]
58%|█████▊ | 117/200 [01:03<00:47, 1.74it/s]
59%|█████▉ | 118/200 [01:03<00:47, 1.74it/s]
60%|█████▉ | 119/200 [01:04<00:46, 1.75it/s]
60%|██████ | 120/200 [01:04<00:45, 1.74it/s]
60%|██████ | 121/200 [01:05<00:45, 1.75it/s]
61%|██████ | 122/200 [01:05<00:44, 1.75it/s]
62%|██████▏ | 123/200 [01:06<00:43, 1.77it/s]
62%|██████▏ | 124/200 [01:07<00:43, 1.76it/s]
62%|██████▎ | 125/200 [01:07<00:42, 1.76it/s]
63%|██████▎ | 126/200 [01:07<00:34, 2.14it/s]
64%|██████▎ | 127/200 [01:08<00:36, 1.98it/s]
64%|██████▍ | 128/200 [01:09<00:37, 1.91it/s]
64%|██████▍ | 129/200 [01:09<00:38, 1.86it/s]
65%|██████▌ | 130/200 [01:10<00:38, 1.83it/s]
66%|██████▌ | 131/200 [01:10<00:38, 1.81it/s]
66%|██████▌ | 132/200 [01:11<00:37, 1.80it/s]
66%|██████▋ | 133/200 [01:11<00:37, 1.79it/s]
67%|██████▋ | 134/200 [01:12<00:36, 1.79it/s]
68%|██████▊ | 135/200 [01:13<00:36, 1.77it/s]
68%|██████▊ | 136/200 [01:13<00:35, 1.78it/s]
68%|██████▊ | 137/200 [01:14<00:35, 1.78it/s]
69%|██████▉ | 138/200 [01:14<00:29, 2.12it/s]
70%|██████▉ | 139/200 [01:14<00:28, 2.13it/s]
70%|███████ | 140/200 [01:15<00:27, 2.19it/s]
70%|███████ | 141/200 [01:15<00:24, 2.39it/s]
71%|███████ | 142/200 [01:15<00:23, 2.50it/s]
72%|███████▏ | 143/200 [01:16<00:23, 2.42it/s]
72%|███████▏ | 144/200 [01:16<00:25, 2.17it/s]
72%|███████▎ | 145/200 [01:17<00:27, 2.02it/s]
73%|███████▎ | 146/200 [01:18<00:27, 1.94it/s]
74%|███████▎ | 147/200 [01:18<00:28, 1.88it/s]
74%|███████▍ | 148/200 [01:19<00:28, 1.84it/s]
74%|███████▍ | 149/200 [01:19<00:28, 1.81it/s]
75%|███████▌ | 150/200 [01:20<00:27, 1.80it/s]
76%|███████▌ | 151/200 [01:20<00:27, 1.79it/s]
76%|███████▌ | 152/200 [01:21<00:26, 1.78it/s]
76%|███████▋ | 153/200 [01:22<00:26, 1.78it/s]
77%|███████▋ | 154/200 [01:22<00:26, 1.76it/s]
78%|███████▊ | 155/200 [01:23<00:25, 1.76it/s]
78%|███████▊ | 156/200 [01:23<00:24, 1.77it/s]
78%|███████▊ | 157/200 [01:24<00:24, 1.77it/s]
79%|███████▉ | 158/200 [01:24<00:23, 1.76it/s]
80%|███████▉ | 159/200 [01:25<00:23, 1.75it/s]
80%|████████ | 160/200 [01:26<00:22, 1.76it/s]
80%|████████ | 161/200 [01:26<00:22, 1.75it/s]
81%|████████ | 162/200 [01:27<00:19, 1.94it/s]
82%|████████▏ | 163/200 [01:27<00:19, 1.88it/s]
82%|████████▏ | 164/200 [01:28<00:19, 1.83it/s]
82%|████████▎ | 165/200 [01:28<00:19, 1.80it/s]
83%|████████▎ | 166/200 [01:29<00:19, 1.78it/s]
84%|████████▎ | 167/200 [01:29<00:18, 1.77it/s]
84%|████████▍ | 168/200 [01:30<00:18, 1.75it/s]
84%|████████▍ | 169/200 [01:31<00:17, 1.75it/s]
85%|████████▌ | 170/200 [01:31<00:17, 1.74it/s]
86%|████████▌ | 171/200 [01:32<00:16, 1.72it/s]
86%|████████▌ | 172/200 [01:32<00:14, 1.89it/s]
86%|████████▋ | 173/200 [01:33<00:14, 1.83it/s]
87%|████████▋ | 174/200 [01:33<00:14, 1.79it/s]
88%|████████▊ | 175/200 [01:34<00:13, 1.85it/s]
88%|████████▊ | 176/200 [01:34<00:13, 1.82it/s]
88%|████████▊ | 177/200 [01:35<00:12, 1.77it/s]
89%|████████▉ | 178/200 [01:36<00:12, 1.76it/s]
90%|████████▉ | 179/200 [01:36<00:11, 1.75it/s]
90%|█████████ | 180/200 [01:37<00:11, 1.74it/s]
90%|█████████ | 181/200 [01:37<00:10, 1.75it/s]
91%|█████████ | 182/200 [01:38<00:10, 1.75it/s]
92%|█████████▏| 183/200 [01:38<00:09, 1.75it/s]
92%|█████████▏| 184/200 [01:39<00:09, 1.73it/s]
92%|█████████▎| 185/200 [01:39<00:07, 1.97it/s]
93%|█████████▎| 186/200 [01:40<00:07, 1.90it/s]
94%|█████████▎| 187/200 [01:41<00:07, 1.84it/s]
94%|█████████▍| 188/200 [01:41<00:06, 1.81it/s]
94%|█████████▍| 189/200 [01:42<00:06, 1.79it/s]
95%|█████████▌| 190/200 [01:42<00:05, 1.76it/s]
96%|█████████▌| 191/200 [01:43<00:05, 1.74it/s]
96%|█████████▌| 192/200 [01:43<00:04, 1.75it/s]
96%|█████████▋| 193/200 [01:44<00:04, 1.74it/s]
97%|█████████▋| 194/200 [01:45<00:03, 1.83it/s]
98%|█████████▊| 195/200 [01:45<00:02, 1.81it/s]
98%|█████████▊| 196/200 [01:46<00:02, 1.79it/s]
98%|█████████▊| 197/200 [01:46<00:01, 1.77it/s]
99%|█████████▉| 198/200 [01:47<00:01, 1.76it/s]
100%|█████████▉| 199/200 [01:47<00:00, 1.76it/s]
100%|██████████| 200/200 [01:48<00:00, 1.75it/s]
100%|██████████| 200/200 [01:48<00:00, 1.84it/s]
- final iteration number: 200
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 108.45662789233029 seconds
----------------------------------------
Analysis formulation: Condat-Vu reconstruction#
#linear_op = WaveletN(wavelet_name="sym8", nb_scales=4)
linear_op = WaveletUD2(
wavelet_id=24,
nb_scale=4,
)
reconstructor = SingleChannelReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='analysis',
verbose=1,
)
WARNING: Making input data immutable.
Lipschitz constant is 17.82847080230713
The lipschitz constraint is satisfied
image_rec, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='condatvu',
num_iterations=100,
)
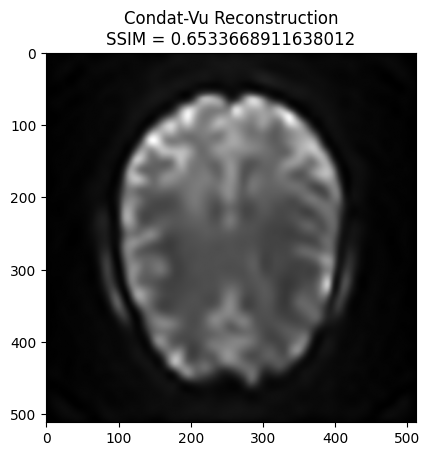
plt.imshow(np.abs(image_rec), cmap='gray')
recon_ssim = ssim(image_rec, image)
plt.title('Condat-Vu Reconstruction\nSSIM = ' + str(recon_ssim))
plt.show()
WARNING: <class 'mri.operators.linear.wavelet.WaveletUD2'> does not inherit an operator parent.
- mu: 6e-07
- lipschitz constant: 17.82847080230713
- tau: 0.10603395407756505
- sigma: 0.5
- rho: 1.0
- std: None
- 1/tau - sigma||L||^2 >= beta/2: True
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletUD2 object at 0x715257d7ba60> - 4
- max iterations: 100
- number of reweights: 0
- primal variable shape: (512, 512)
- dual variable shape: (2621440,)
----------------------------------------
Starting optimization...
0%| | 0/100 [00:00<?, ?it/s]
1%| | 1/100 [00:02<04:20, 2.63s/it]
2%|▏ | 2/100 [00:05<04:15, 2.60s/it]
3%|▎ | 3/100 [00:07<04:02, 2.50s/it]
4%|▍ | 4/100 [00:10<04:00, 2.51s/it]
5%|▌ | 5/100 [00:12<03:58, 2.51s/it]
6%|▌ | 6/100 [00:15<04:01, 2.57s/it]
7%|▋ | 7/100 [00:17<03:59, 2.57s/it]
8%|▊ | 8/100 [00:20<03:55, 2.55s/it]
9%|▉ | 9/100 [00:22<03:51, 2.55s/it]
10%|█ | 10/100 [00:25<03:48, 2.54s/it]
11%|█ | 11/100 [00:27<03:45, 2.53s/it]
12%|█▏ | 12/100 [00:30<03:41, 2.52s/it]
13%|█▎ | 13/100 [00:32<03:38, 2.52s/it]
14%|█▍ | 14/100 [00:35<03:42, 2.58s/it]
15%|█▌ | 15/100 [00:38<03:38, 2.57s/it]
16%|█▌ | 16/100 [00:40<03:35, 2.56s/it]
17%|█▋ | 17/100 [00:43<03:31, 2.55s/it]
18%|█▊ | 18/100 [00:45<03:27, 2.53s/it]
19%|█▉ | 19/100 [00:48<03:21, 2.48s/it]
20%|██ | 20/100 [00:50<03:19, 2.50s/it]
21%|██ | 21/100 [00:53<03:22, 2.56s/it]
22%|██▏ | 22/100 [00:55<03:20, 2.57s/it]
23%|██▎ | 23/100 [00:58<03:17, 2.56s/it]
24%|██▍ | 24/100 [01:01<03:13, 2.55s/it]
25%|██▌ | 25/100 [01:03<03:11, 2.55s/it]
26%|██▌ | 26/100 [01:06<03:07, 2.54s/it]
27%|██▋ | 27/100 [01:08<03:04, 2.53s/it]
28%|██▊ | 28/100 [01:11<03:01, 2.52s/it]
29%|██▉ | 29/100 [01:13<03:02, 2.57s/it]
30%|███ | 30/100 [01:16<02:58, 2.55s/it]
31%|███ | 31/100 [01:18<02:55, 2.55s/it]
32%|███▏ | 32/100 [01:21<02:52, 2.54s/it]
33%|███▎ | 33/100 [01:23<02:49, 2.53s/it]
34%|███▍ | 34/100 [01:26<02:46, 2.52s/it]
35%|███▌ | 35/100 [01:28<02:44, 2.53s/it]
36%|███▌ | 36/100 [01:31<02:42, 2.53s/it]
37%|███▋ | 37/100 [01:34<02:39, 2.54s/it]
38%|███▊ | 38/100 [01:36<02:37, 2.53s/it]
39%|███▉ | 39/100 [01:39<02:33, 2.52s/it]
40%|████ | 40/100 [01:41<02:31, 2.52s/it]
41%|████ | 41/100 [01:43<02:25, 2.46s/it]
42%|████▏ | 42/100 [01:46<02:23, 2.48s/it]
43%|████▎ | 43/100 [01:48<02:21, 2.48s/it]
44%|████▍ | 44/100 [01:51<02:18, 2.48s/it]
45%|████▌ | 45/100 [01:53<02:16, 2.49s/it]
46%|████▌ | 46/100 [01:56<02:14, 2.49s/it]
47%|████▋ | 47/100 [01:58<02:11, 2.48s/it]
48%|████▊ | 48/100 [02:01<02:08, 2.48s/it]
49%|████▉ | 49/100 [02:03<02:09, 2.53s/it]
50%|█████ | 50/100 [02:06<02:09, 2.60s/it]
51%|█████ | 51/100 [02:09<02:06, 2.59s/it]
52%|█████▏ | 52/100 [02:11<02:02, 2.56s/it]
53%|█████▎ | 53/100 [02:14<01:58, 2.52s/it]
54%|█████▍ | 54/100 [02:16<01:55, 2.51s/it]
55%|█████▌ | 55/100 [02:19<01:53, 2.53s/it]
56%|█████▌ | 56/100 [02:21<01:50, 2.51s/it]
57%|█████▋ | 57/100 [02:24<01:47, 2.50s/it]
58%|█████▊ | 58/100 [02:26<01:44, 2.49s/it]
59%|█████▉ | 59/100 [02:29<01:41, 2.48s/it]
60%|██████ | 60/100 [02:31<01:38, 2.47s/it]
61%|██████ | 61/100 [02:34<01:36, 2.46s/it]
62%|██████▏ | 62/100 [02:36<01:33, 2.46s/it]
63%|██████▎ | 63/100 [02:39<01:32, 2.49s/it]
64%|██████▍ | 64/100 [02:41<01:29, 2.48s/it]
65%|██████▌ | 65/100 [02:43<01:26, 2.48s/it]
66%|██████▌ | 66/100 [02:46<01:23, 2.47s/it]
67%|██████▋ | 67/100 [02:48<01:21, 2.47s/it]
68%|██████▊ | 68/100 [02:51<01:20, 2.51s/it]
69%|██████▉ | 69/100 [02:54<01:18, 2.54s/it]
70%|███████ | 70/100 [02:56<01:16, 2.55s/it]
71%|███████ | 71/100 [02:59<01:13, 2.52s/it]
72%|███████▏ | 72/100 [03:01<01:10, 2.50s/it]
73%|███████▎ | 73/100 [03:03<01:05, 2.44s/it]
74%|███████▍ | 74/100 [03:06<01:04, 2.47s/it]
75%|███████▌ | 75/100 [03:08<01:01, 2.47s/it]
76%|███████▌ | 76/100 [03:11<00:59, 2.47s/it]
77%|███████▋ | 77/100 [03:13<00:56, 2.46s/it]
78%|███████▊ | 78/100 [03:16<00:54, 2.47s/it]
79%|███████▉ | 79/100 [03:18<00:52, 2.48s/it]
80%|████████ | 80/100 [03:21<00:49, 2.48s/it]
81%|████████ | 81/100 [03:23<00:46, 2.46s/it]
82%|████████▏ | 82/100 [03:26<00:44, 2.46s/it]
83%|████████▎ | 83/100 [03:28<00:41, 2.46s/it]
84%|████████▍ | 84/100 [03:31<00:39, 2.46s/it]
85%|████████▌ | 85/100 [03:33<00:37, 2.47s/it]
86%|████████▌ | 86/100 [03:35<00:34, 2.47s/it]
87%|████████▋ | 87/100 [03:38<00:32, 2.46s/it]
88%|████████▊ | 88/100 [03:40<00:29, 2.46s/it]
89%|████████▉ | 89/100 [03:43<00:26, 2.39s/it]
90%|█████████ | 90/100 [03:45<00:24, 2.42s/it]
91%|█████████ | 91/100 [03:48<00:22, 2.50s/it]
92%|█████████▏| 92/100 [03:50<00:19, 2.44s/it]
93%|█████████▎| 93/100 [03:53<00:17, 2.45s/it]
94%|█████████▍| 94/100 [03:55<00:14, 2.39s/it]
95%|█████████▌| 95/100 [03:57<00:12, 2.41s/it]
96%|█████████▌| 96/100 [04:00<00:09, 2.45s/it]
97%|█████████▋| 97/100 [04:02<00:07, 2.40s/it]
98%|█████████▊| 98/100 [04:05<00:04, 2.45s/it]
99%|█████████▉| 99/100 [04:07<00:02, 2.45s/it]
100%|██████████| 100/100 [04:10<00:00, 2.47s/it]
100%|██████████| 100/100 [04:10<00:00, 2.50s/it]
- final iteration number: 100
- final cost value: 1000000.0
- converged: False
Done.
Execution time: 252.37198956031352 seconds
----------------------------------------