14. Deep learning MRI reconstructoion: Simple UNet model.#
This model is a simplified version of the U-Net architecture, which is widely used for image segmentation tasks. This is implemented in the proprietary FASTMRI package [fastmri]_.
The U-Net model consists of an encoder (downsampling path) and a decoder (upsampling path) with skip connections between corresponding layers in the encoder and decoder. These skip connections help in retaining spatial information that is lost during the downsampling process.
The primary purpose of this model is to perform image reconstruction tasks, specifically for MRI images. It takes an input MRI image and reconstructs it to improve the image quality or to recover missing parts of the image.
This implementation of the UNet model was pulled from the FastMRI Facebook repository, which is a collaborative research project aimed at advancing the field of medical imaging using machine learning techniques.
where \(\mathbf{\hat{x}}\) is the reconstructed MRI image, \(\mathbf{x}\) is the ground truth image, \(\mathbf{y}\) is the input MRI image (e.g., k-space data), and \(\mathcal{U}_\mathbf{\theta}\) is the U-Net model parameterized by \(\theta\).
.. warning:: We train on a single image here. In practice, this should be done on a database like fastMRI [fastmri]_. “””
%%#
.. colab-link::#
:needs_gpu: 1#
#
!pip install mri-nufft[gpunufft] scikit-image fastmri#
Author: Zaccharie Ramzi, Chaithya G R, Pierre-Antoine Comby
Date: 01/07/2021
Target: ATSI MSc students, Paris-Saclay University
# Package import
from mri.operators import FFT, WaveletN, OWL
from mri.reconstructors import CalibrationlessReconstructor
from pysap.data import get_sample_data
# Third party import
from modopt.opt.proximity import GroupLASSO
from modopt.math.metrics import ssim
import numpy as np
import matplotlib.pyplot as plt
/volatile/github-ci-mind-inria/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
# Loading input data
cartesian_ref_image = get_sample_data('2d-pmri').data
image = np.linalg.norm(cartesian_ref_image, axis=0)
# Obtain MRI cartesian mask
mask = get_sample_data("cartesian-mri-mask").data
# View Input
plt.subplot(1, 2, 1)
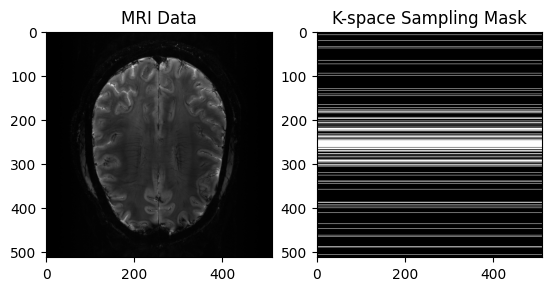
plt.imshow(np.abs(image), cmap='gray')
plt.title("MRI Data")
plt.subplot(1, 2, 2)
plt.imshow(mask, cmap='gray')
plt.title("K-space Sampling Mask")
plt.show()
Generate the kspace#
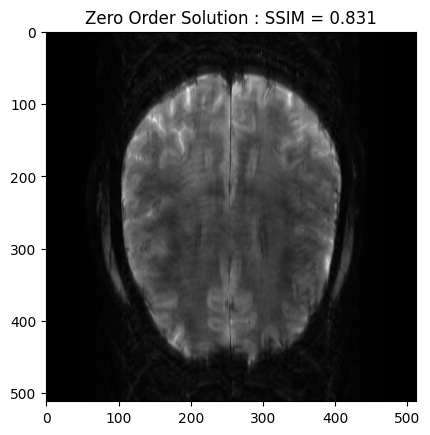
From the 2D brain slice and the acquisition mask, we retrospectively undersample the k-space using a cartesian acquisition mask We then reconstruct the zero order solution as a baseline
# Get the locations of the kspace samples and the associated observations
fourier_op = FFT(mask=mask, shape=image.shape,
n_coils=cartesian_ref_image.shape[0])
kspace_obs = fourier_op.op(cartesian_ref_image)
# Zero order solution
zero_soln = np.linalg.norm(fourier_op.adj_op(kspace_obs), axis=0)
base_ssim = ssim(zero_soln, image)
plt.imshow(np.abs(zero_soln), cmap='gray')
plt.title('Zero Order Solution : SSIM = ' + str(np.around(base_ssim, 3)))
plt.show()
Synthesis formulation: FISTA vs POGM optimization#
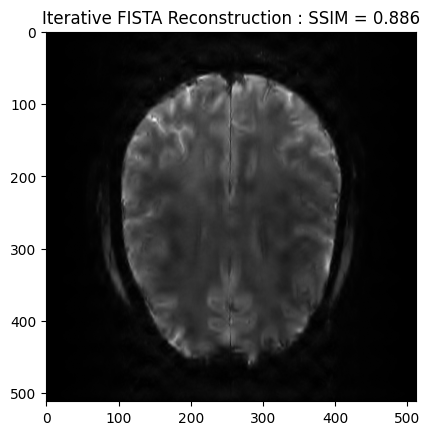
We now want to refine the zero order solution using a FISTA optimization. The cost function is set to Proximity Cost + Gradient Cost
# Setup the operators
linear_op = WaveletN(
wavelet_name='sym8',
nb_scale=4,
n_coils=cartesian_ref_image.shape[0],
)
coeffs = linear_op.op(cartesian_ref_image)
regularizer_op = GroupLASSO(weights=6e-8)
Setup reconstructor:#
# Setup Reconstructor
reconstructor = CalibrationlessReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='synthesis',
verbose=1,
)
WARNING: Making input data immutable.
Lipschitz constant is 1.1
The lipschitz constraint is satisfied
# Run the FISTA reconstruction and view results
image_rec, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='fista',
num_iterations=100,
)
image_rec = np.linalg.norm(image_rec, axis=0)
recon_ssim = ssim(image_rec, image)
plt.imshow(np.abs(image_rec), cmap='gray')
plt.title('Iterative FISTA Reconstruction : SSIM = ' + str(np.around(recon_ssim, 3)))
plt.show()
WARNING: Making input data immutable.
- mu: 6e-08
- lipschitz constant: 1.1
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7718fafb1060> - 4
- max iterations: 100
- image variable shape: (512, 512)
- alpha variable shape: (32, 291721)
----------------------------------------
Starting optimization...
0%| | 0/100 [00:00<?, ?it/s]
1%| | 1/100 [00:02<03:29, 2.12s/it]
2%|▏ | 2/100 [00:04<03:26, 2.10s/it]
3%|▎ | 3/100 [00:06<03:23, 2.10s/it]
4%|▍ | 4/100 [00:08<03:21, 2.10s/it]
5%|▌ | 5/100 [00:10<03:19, 2.10s/it]
6%|▌ | 6/100 [00:12<03:17, 2.10s/it]
7%|▋ | 7/100 [00:14<03:15, 2.10s/it]
8%|▊ | 8/100 [00:16<03:13, 2.10s/it]
9%|▉ | 9/100 [00:18<03:11, 2.10s/it]
10%|█ | 10/100 [00:21<03:09, 2.10s/it]
11%|█ | 11/100 [00:23<03:07, 2.10s/it]
12%|█▏ | 12/100 [00:25<03:05, 2.10s/it]
13%|█▎ | 13/100 [00:27<03:03, 2.10s/it]
14%|█▍ | 14/100 [00:29<03:00, 2.10s/it]
15%|█▌ | 15/100 [00:31<02:58, 2.10s/it]
16%|█▌ | 16/100 [00:33<02:56, 2.10s/it]
17%|█▋ | 17/100 [00:35<02:54, 2.11s/it]
18%|█▊ | 18/100 [00:37<02:52, 2.10s/it]
19%|█▉ | 19/100 [00:39<02:49, 2.09s/it]
20%|██ | 20/100 [00:42<02:47, 2.09s/it]
21%|██ | 21/100 [00:44<02:45, 2.09s/it]
22%|██▏ | 22/100 [00:46<02:42, 2.09s/it]
23%|██▎ | 23/100 [00:48<02:40, 2.09s/it]
24%|██▍ | 24/100 [00:50<02:38, 2.08s/it]
25%|██▌ | 25/100 [00:52<02:36, 2.09s/it]
26%|██▌ | 26/100 [00:54<02:34, 2.09s/it]
27%|██▋ | 27/100 [00:56<02:32, 2.09s/it]
28%|██▊ | 28/100 [00:58<02:30, 2.09s/it]
29%|██▉ | 29/100 [01:00<02:28, 2.09s/it]
30%|███ | 30/100 [01:02<02:26, 2.09s/it]
31%|███ | 31/100 [01:04<02:24, 2.09s/it]
32%|███▏ | 32/100 [01:07<02:22, 2.09s/it]
33%|███▎ | 33/100 [01:09<02:19, 2.08s/it]
34%|███▍ | 34/100 [01:11<02:17, 2.08s/it]
35%|███▌ | 35/100 [01:13<02:15, 2.08s/it]
36%|███▌ | 36/100 [01:15<02:13, 2.08s/it]
37%|███▋ | 37/100 [01:17<02:11, 2.08s/it]
38%|███▊ | 38/100 [01:19<02:09, 2.08s/it]
39%|███▉ | 39/100 [01:21<02:07, 2.09s/it]
40%|████ | 40/100 [01:23<02:05, 2.09s/it]
41%|████ | 41/100 [01:25<02:03, 2.09s/it]
42%|████▏ | 42/100 [01:27<02:01, 2.09s/it]
43%|████▎ | 43/100 [01:29<01:58, 2.08s/it]
44%|████▍ | 44/100 [01:32<01:56, 2.09s/it]
45%|████▌ | 45/100 [01:34<01:54, 2.09s/it]
46%|████▌ | 46/100 [01:36<01:52, 2.09s/it]
47%|████▋ | 47/100 [01:38<01:50, 2.09s/it]
48%|████▊ | 48/100 [01:40<01:48, 2.09s/it]
49%|████▉ | 49/100 [01:42<01:46, 2.09s/it]
50%|█████ | 50/100 [01:44<01:44, 2.09s/it]
51%|█████ | 51/100 [01:46<01:42, 2.09s/it]
52%|█████▏ | 52/100 [01:48<01:40, 2.09s/it]
53%|█████▎ | 53/100 [01:50<01:37, 2.08s/it]
54%|█████▍ | 54/100 [01:52<01:35, 2.09s/it]
55%|█████▌ | 55/100 [01:55<01:33, 2.09s/it]
56%|█████▌ | 56/100 [01:57<01:31, 2.09s/it]
57%|█████▋ | 57/100 [01:59<01:29, 2.09s/it]
58%|█████▊ | 58/100 [02:01<01:27, 2.09s/it]
59%|█████▉ | 59/100 [02:03<01:25, 2.09s/it]
60%|██████ | 60/100 [02:05<01:23, 2.09s/it]
61%|██████ | 61/100 [02:07<01:21, 2.08s/it]
62%|██████▏ | 62/100 [02:09<01:19, 2.08s/it]
63%|██████▎ | 63/100 [02:11<01:17, 2.09s/it]
64%|██████▍ | 64/100 [02:13<01:14, 2.08s/it]
65%|██████▌ | 65/100 [02:15<01:12, 2.08s/it]
66%|██████▌ | 66/100 [02:17<01:10, 2.08s/it]
67%|██████▋ | 67/100 [02:20<01:08, 2.08s/it]
68%|██████▊ | 68/100 [02:22<01:06, 2.08s/it]
69%|██████▉ | 69/100 [02:24<01:04, 2.08s/it]
70%|███████ | 70/100 [02:26<01:02, 2.09s/it]
71%|███████ | 71/100 [02:28<01:00, 2.09s/it]
72%|███████▏ | 72/100 [02:30<00:58, 2.09s/it]
73%|███████▎ | 73/100 [02:32<00:56, 2.09s/it]
74%|███████▍ | 74/100 [02:34<00:54, 2.09s/it]
75%|███████▌ | 75/100 [02:36<00:52, 2.08s/it]
76%|███████▌ | 76/100 [02:38<00:49, 2.08s/it]
77%|███████▋ | 77/100 [02:40<00:47, 2.08s/it]
78%|███████▊ | 78/100 [02:42<00:45, 2.08s/it]
79%|███████▉ | 79/100 [02:45<00:43, 2.08s/it]
80%|████████ | 80/100 [02:47<00:41, 2.08s/it]
81%|████████ | 81/100 [02:49<00:39, 2.08s/it]
82%|████████▏ | 82/100 [02:51<00:37, 2.09s/it]
83%|████████▎ | 83/100 [02:53<00:35, 2.09s/it]
84%|████████▍ | 84/100 [02:55<00:33, 2.09s/it]
85%|████████▌ | 85/100 [02:57<00:31, 2.08s/it]
86%|████████▌ | 86/100 [02:59<00:29, 2.09s/it]
87%|████████▋ | 87/100 [03:01<00:27, 2.09s/it]
88%|████████▊ | 88/100 [03:03<00:25, 2.09s/it]
89%|████████▉ | 89/100 [03:05<00:22, 2.09s/it]
90%|█████████ | 90/100 [03:08<00:20, 2.09s/it]
91%|█████████ | 91/100 [03:10<00:18, 2.09s/it]
92%|█████████▏| 92/100 [03:12<00:16, 2.09s/it]
93%|█████████▎| 93/100 [03:14<00:14, 2.09s/it]
94%|█████████▍| 94/100 [03:16<00:12, 2.09s/it]
95%|█████████▌| 95/100 [03:18<00:10, 2.09s/it]
96%|█████████▌| 96/100 [03:20<00:08, 2.09s/it]
97%|█████████▋| 97/100 [03:22<00:06, 2.09s/it]
98%|█████████▊| 98/100 [03:24<00:04, 2.09s/it]
99%|█████████▉| 99/100 [03:26<00:02, 2.08s/it]
100%|██████████| 100/100 [03:28<00:00, 2.09s/it]
100%|██████████| 100/100 [03:28<00:00, 2.09s/it]
- final iteration number: 100
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 208.89562634564936 seconds
----------------------------------------
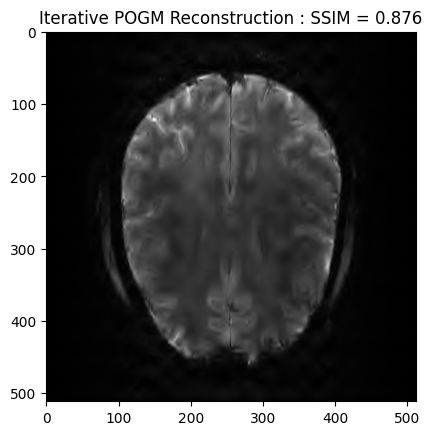
POGM optimization#
# Run the POGM reconstruction and view results
image_rec2, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='pogm',
num_iterations=100,
)
image_rec2 = np.linalg.norm(image_rec2, axis=0)
recon2_ssim = ssim(image_rec2, image)
plt.imshow(np.abs(image_rec2), cmap='gray')
plt.title('Iterative POGM Reconstruction : SSIM = ' + str(np.around(recon2_ssim, 3)))
plt.show()
- mu: 6e-08
- lipschitz constant: 1.1
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7718fafb1060> - 4
- max iterations: 100
- image variable shape: (32, 512, 512)
----------------------------------------
Starting optimization...
0%| | 0/100 [00:00<?, ?it/s]
1%| | 1/100 [00:02<03:56, 2.39s/it]
2%|▏ | 2/100 [00:04<03:55, 2.40s/it]
3%|▎ | 3/100 [00:07<03:52, 2.39s/it]
4%|▍ | 4/100 [00:09<03:49, 2.39s/it]
5%|▌ | 5/100 [00:11<03:46, 2.39s/it]
6%|▌ | 6/100 [00:14<03:45, 2.39s/it]
7%|▋ | 7/100 [00:16<03:42, 2.40s/it]
8%|▊ | 8/100 [00:19<03:41, 2.41s/it]
9%|▉ | 9/100 [00:21<03:39, 2.42s/it]
10%|█ | 10/100 [00:24<03:37, 2.42s/it]
11%|█ | 11/100 [00:26<03:34, 2.41s/it]
12%|█▏ | 12/100 [00:28<03:32, 2.42s/it]
13%|█▎ | 13/100 [00:31<03:30, 2.42s/it]
14%|█▍ | 14/100 [00:33<03:28, 2.42s/it]
15%|█▌ | 15/100 [00:36<03:25, 2.42s/it]
16%|█▌ | 16/100 [00:38<03:22, 2.41s/it]
17%|█▋ | 17/100 [00:41<03:22, 2.44s/it]
18%|█▊ | 18/100 [00:43<03:19, 2.44s/it]
19%|█▉ | 19/100 [00:46<03:23, 2.52s/it]
20%|██ | 20/100 [00:50<03:53, 2.92s/it]
21%|██ | 21/100 [00:53<04:09, 3.16s/it]
22%|██▏ | 22/100 [00:57<04:14, 3.26s/it]
23%|██▎ | 23/100 [01:00<04:13, 3.29s/it]
24%|██▍ | 24/100 [01:03<04:10, 3.29s/it]
25%|██▌ | 25/100 [01:07<04:12, 3.36s/it]
26%|██▌ | 26/100 [01:10<04:13, 3.42s/it]
27%|██▋ | 27/100 [01:14<04:16, 3.52s/it]
28%|██▊ | 28/100 [01:18<04:13, 3.53s/it]
29%|██▉ | 29/100 [01:20<03:47, 3.21s/it]
30%|███ | 30/100 [01:23<03:27, 2.97s/it]
31%|███ | 31/100 [01:25<03:13, 2.80s/it]
32%|███▏ | 32/100 [01:27<03:02, 2.69s/it]
33%|███▎ | 33/100 [01:30<02:55, 2.62s/it]
34%|███▍ | 34/100 [01:32<02:49, 2.57s/it]
35%|███▌ | 35/100 [01:35<02:44, 2.52s/it]
36%|███▌ | 36/100 [01:37<02:39, 2.50s/it]
37%|███▋ | 37/100 [01:40<02:36, 2.48s/it]
38%|███▊ | 38/100 [01:42<02:32, 2.47s/it]
39%|███▉ | 39/100 [01:45<02:30, 2.47s/it]
40%|████ | 40/100 [01:47<02:27, 2.46s/it]
41%|████ | 41/100 [01:49<02:24, 2.45s/it]
42%|████▏ | 42/100 [01:52<02:21, 2.44s/it]
43%|████▎ | 43/100 [01:54<02:18, 2.43s/it]
44%|████▍ | 44/100 [01:57<02:15, 2.43s/it]
45%|████▌ | 45/100 [01:59<02:13, 2.42s/it]
46%|████▌ | 46/100 [02:02<02:11, 2.44s/it]
47%|████▋ | 47/100 [02:04<02:09, 2.45s/it]
48%|████▊ | 48/100 [02:07<02:07, 2.45s/it]
49%|████▉ | 49/100 [02:09<02:05, 2.46s/it]
50%|█████ | 50/100 [02:11<02:02, 2.46s/it]
51%|█████ | 51/100 [02:14<02:03, 2.53s/it]
52%|█████▏ | 52/100 [02:17<02:02, 2.55s/it]
53%|█████▎ | 53/100 [02:19<01:59, 2.55s/it]
54%|█████▍ | 54/100 [02:22<01:57, 2.55s/it]
55%|█████▌ | 55/100 [02:24<01:54, 2.55s/it]
56%|█████▌ | 56/100 [02:27<01:52, 2.56s/it]
57%|█████▋ | 57/100 [02:30<01:50, 2.56s/it]
58%|█████▊ | 58/100 [02:32<01:47, 2.56s/it]
59%|█████▉ | 59/100 [02:35<01:44, 2.56s/it]
60%|██████ | 60/100 [02:37<01:42, 2.56s/it]
61%|██████ | 61/100 [02:40<01:40, 2.57s/it]
62%|██████▏ | 62/100 [02:42<01:37, 2.56s/it]
63%|██████▎ | 63/100 [02:45<01:34, 2.57s/it]
64%|██████▍ | 64/100 [02:48<01:32, 2.57s/it]
65%|██████▌ | 65/100 [02:50<01:29, 2.57s/it]
66%|██████▌ | 66/100 [02:53<01:27, 2.57s/it]
67%|██████▋ | 67/100 [02:55<01:24, 2.57s/it]
68%|██████▊ | 68/100 [02:58<01:22, 2.57s/it]
69%|██████▉ | 69/100 [03:00<01:19, 2.57s/it]
70%|███████ | 70/100 [03:03<01:17, 2.57s/it]
71%|███████ | 71/100 [03:06<01:14, 2.57s/it]
72%|███████▏ | 72/100 [03:08<01:12, 2.57s/it]
73%|███████▎ | 73/100 [03:11<01:09, 2.58s/it]
74%|███████▍ | 74/100 [03:13<01:06, 2.57s/it]
75%|███████▌ | 75/100 [03:16<01:04, 2.58s/it]
76%|███████▌ | 76/100 [03:18<01:02, 2.59s/it]
77%|███████▋ | 77/100 [03:21<00:59, 2.60s/it]
78%|███████▊ | 78/100 [03:24<00:56, 2.59s/it]
79%|███████▉ | 79/100 [03:26<00:54, 2.59s/it]
80%|████████ | 80/100 [03:29<00:51, 2.59s/it]
81%|████████ | 81/100 [03:31<00:49, 2.59s/it]
82%|████████▏ | 82/100 [03:34<00:46, 2.59s/it]
83%|████████▎ | 83/100 [03:37<00:43, 2.59s/it]
84%|████████▍ | 84/100 [03:39<00:41, 2.57s/it]
85%|████████▌ | 85/100 [03:42<00:38, 2.56s/it]
86%|████████▌ | 86/100 [03:44<00:35, 2.55s/it]
87%|████████▋ | 87/100 [03:47<00:33, 2.55s/it]
88%|████████▊ | 88/100 [03:49<00:30, 2.54s/it]
89%|████████▉ | 89/100 [03:52<00:27, 2.54s/it]
90%|█████████ | 90/100 [03:54<00:25, 2.57s/it]
91%|█████████ | 91/100 [03:57<00:22, 2.54s/it]
92%|█████████▏| 92/100 [03:59<00:20, 2.51s/it]
93%|█████████▎| 93/100 [04:02<00:17, 2.49s/it]
94%|█████████▍| 94/100 [04:04<00:14, 2.48s/it]
95%|█████████▌| 95/100 [04:07<00:12, 2.47s/it]
96%|█████████▌| 96/100 [04:09<00:09, 2.47s/it]
97%|█████████▋| 97/100 [04:12<00:07, 2.47s/it]
98%|█████████▊| 98/100 [04:14<00:04, 2.46s/it]
99%|█████████▉| 99/100 [04:17<00:02, 2.47s/it]
100%|██████████| 100/100 [04:19<00:00, 2.45s/it]
100%|██████████| 100/100 [04:19<00:00, 2.59s/it]
- final iteration number: 100
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 259.48065809812397 seconds
----------------------------------------
# Setup the operators
linear_op = WaveletN(
wavelet_name='sym8',
nb_scale=4,
n_coils=cartesian_ref_image.shape[0],
)
coeffs = linear_op.op(cartesian_ref_image)
regularizer_op = OWL(
alpha=1.05e-8,
beta=0,
mode='band_based',
n_coils=cartesian_ref_image.shape[0],
bands_shape=linear_op.coeffs_shape,
)
# Setup Reconstructor
reconstructor = CalibrationlessReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='synthesis',
verbose=1,
)
WARNING: Making input data immutable.
Lipschitz constant is 1.0999999344348907
The lipschitz constraint is satisfied
# Run the FISTA reconstruction and view results
image_rec, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='fista',
num_iterations=100,
)
image_rec = np.linalg.norm(image_rec, axis=0)
recon_ssim = ssim(image_rec, image)
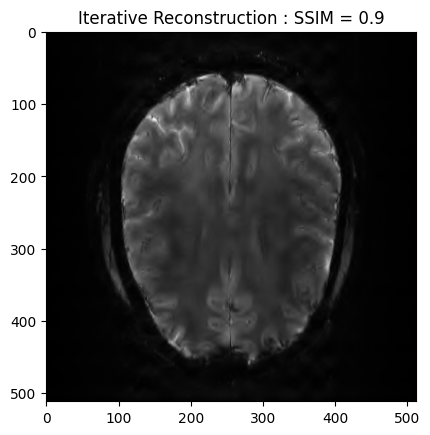
plt.imshow(np.abs(image_rec), cmap='gray')
plt.title('Iterative Reconstruction : SSIM = ' + str(np.around(recon_ssim, 2)))
plt.show()
- mu: [<modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fa5a0f10>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fa5a00a0>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fa5a0160>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fb989ab0>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fb98bc40>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fb989e40>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fb989ae0>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fb989d80>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fafccbb0>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fafcc9a0>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718faf16f50>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x771a0cff4c10>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x771a0cff4b20>]
- lipschitz constant: 1.0999999344348907
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7718fa5a0130> - 4
- max iterations: 100
- image variable shape: (512, 512)
- alpha variable shape: (32, 291721)
----------------------------------------
Starting optimization...
0%| | 0/100 [00:00<?, ?it/s]
1%| | 1/100 [00:03<05:39, 3.43s/it]
2%|▏ | 2/100 [00:06<05:37, 3.44s/it]
3%|▎ | 3/100 [00:10<05:36, 3.47s/it]
4%|▍ | 4/100 [00:13<05:34, 3.48s/it]
5%|▌ | 5/100 [00:17<05:29, 3.47s/it]
6%|▌ | 6/100 [00:20<05:22, 3.43s/it]
7%|▋ | 7/100 [00:24<05:21, 3.46s/it]
8%|▊ | 8/100 [00:27<05:21, 3.49s/it]
9%|▉ | 9/100 [00:31<05:17, 3.49s/it]
10%|█ | 10/100 [00:34<05:13, 3.49s/it]
11%|█ | 11/100 [00:38<05:10, 3.49s/it]
12%|█▏ | 12/100 [00:41<05:06, 3.48s/it]
13%|█▎ | 13/100 [00:45<05:03, 3.48s/it]
14%|█▍ | 14/100 [00:48<04:58, 3.47s/it]
15%|█▌ | 15/100 [00:52<04:54, 3.47s/it]
16%|█▌ | 16/100 [00:55<04:49, 3.45s/it]
17%|█▋ | 17/100 [00:58<04:44, 3.43s/it]
18%|█▊ | 18/100 [01:02<04:38, 3.40s/it]
19%|█▉ | 19/100 [01:05<04:32, 3.36s/it]
20%|██ | 20/100 [01:08<04:27, 3.34s/it]
21%|██ | 21/100 [01:12<04:23, 3.34s/it]
22%|██▏ | 22/100 [01:15<04:19, 3.33s/it]
23%|██▎ | 23/100 [01:18<04:15, 3.32s/it]
24%|██▍ | 24/100 [01:21<04:10, 3.30s/it]
25%|██▌ | 25/100 [01:25<04:04, 3.26s/it]
26%|██▌ | 26/100 [01:28<03:57, 3.20s/it]
27%|██▋ | 27/100 [01:31<03:50, 3.16s/it]
28%|██▊ | 28/100 [01:34<03:44, 3.12s/it]
29%|██▉ | 29/100 [01:37<03:40, 3.10s/it]
30%|███ | 30/100 [01:40<03:35, 3.08s/it]
31%|███ | 31/100 [01:43<03:31, 3.07s/it]
32%|███▏ | 32/100 [01:46<03:27, 3.06s/it]
33%|███▎ | 33/100 [01:49<03:24, 3.06s/it]
34%|███▍ | 34/100 [01:52<03:21, 3.05s/it]
35%|███▌ | 35/100 [01:55<03:18, 3.05s/it]
36%|███▌ | 36/100 [01:58<03:14, 3.05s/it]
37%|███▋ | 37/100 [02:01<03:11, 3.05s/it]
38%|███▊ | 38/100 [02:04<03:08, 3.04s/it]
39%|███▉ | 39/100 [02:07<03:05, 3.04s/it]
40%|████ | 40/100 [02:10<03:02, 3.04s/it]
41%|████ | 41/100 [02:13<02:59, 3.04s/it]
42%|████▏ | 42/100 [02:16<02:56, 3.04s/it]
43%|████▎ | 43/100 [02:19<02:53, 3.04s/it]
44%|████▍ | 44/100 [02:22<02:50, 3.04s/it]
45%|████▌ | 45/100 [02:25<02:47, 3.04s/it]
46%|████▌ | 46/100 [02:29<02:44, 3.04s/it]
47%|████▋ | 47/100 [02:32<02:41, 3.04s/it]
48%|████▊ | 48/100 [02:35<02:38, 3.04s/it]
49%|████▉ | 49/100 [02:38<02:35, 3.05s/it]
50%|█████ | 50/100 [02:41<02:32, 3.04s/it]
51%|█████ | 51/100 [02:44<02:29, 3.05s/it]
52%|█████▏ | 52/100 [02:47<02:26, 3.05s/it]
53%|█████▎ | 53/100 [02:50<02:23, 3.05s/it]
54%|█████▍ | 54/100 [02:53<02:20, 3.05s/it]
55%|█████▌ | 55/100 [02:56<02:17, 3.05s/it]
56%|█████▌ | 56/100 [02:59<02:14, 3.05s/it]
57%|█████▋ | 57/100 [03:02<02:11, 3.05s/it]
58%|█████▊ | 58/100 [03:05<02:07, 3.05s/it]
59%|█████▉ | 59/100 [03:08<02:04, 3.04s/it]
60%|██████ | 60/100 [03:11<02:01, 3.04s/it]
61%|██████ | 61/100 [03:14<01:58, 3.04s/it]
62%|██████▏ | 62/100 [03:17<01:55, 3.04s/it]
63%|██████▎ | 63/100 [03:20<01:52, 3.05s/it]
64%|██████▍ | 64/100 [03:23<01:49, 3.05s/it]
65%|██████▌ | 65/100 [03:26<01:46, 3.05s/it]
66%|██████▌ | 66/100 [03:29<01:43, 3.04s/it]
67%|██████▋ | 67/100 [03:32<01:40, 3.05s/it]
68%|██████▊ | 68/100 [03:36<01:37, 3.04s/it]
69%|██████▉ | 69/100 [03:39<01:34, 3.05s/it]
70%|███████ | 70/100 [03:42<01:31, 3.05s/it]
71%|███████ | 71/100 [03:45<01:28, 3.05s/it]
72%|███████▏ | 72/100 [03:48<01:25, 3.05s/it]
73%|███████▎ | 73/100 [03:51<01:22, 3.05s/it]
74%|███████▍ | 74/100 [03:54<01:19, 3.05s/it]
75%|███████▌ | 75/100 [03:57<01:16, 3.06s/it]
76%|███████▌ | 76/100 [04:00<01:13, 3.05s/it]
77%|███████▋ | 77/100 [04:03<01:10, 3.05s/it]
78%|███████▊ | 78/100 [04:06<01:07, 3.05s/it]
79%|███████▉ | 79/100 [04:09<01:04, 3.05s/it]
80%|████████ | 80/100 [04:12<01:01, 3.05s/it]
81%|████████ | 81/100 [04:15<00:57, 3.05s/it]
82%|████████▏ | 82/100 [04:18<00:54, 3.05s/it]
83%|████████▎ | 83/100 [04:21<00:51, 3.05s/it]
84%|████████▍ | 84/100 [04:24<00:48, 3.05s/it]
85%|████████▌ | 85/100 [04:27<00:45, 3.05s/it]
86%|████████▌ | 86/100 [04:30<00:42, 3.04s/it]
87%|████████▋ | 87/100 [04:33<00:39, 3.04s/it]
88%|████████▊ | 88/100 [04:37<00:36, 3.04s/it]
89%|████████▉ | 89/100 [04:40<00:33, 3.05s/it]
90%|█████████ | 90/100 [04:43<00:30, 3.07s/it]
91%|█████████ | 91/100 [04:46<00:27, 3.09s/it]
92%|█████████▏| 92/100 [04:49<00:24, 3.11s/it]
93%|█████████▎| 93/100 [04:52<00:21, 3.12s/it]
94%|█████████▍| 94/100 [04:55<00:18, 3.13s/it]
95%|█████████▌| 95/100 [04:58<00:15, 3.14s/it]
96%|█████████▌| 96/100 [05:02<00:12, 3.14s/it]
97%|█████████▋| 97/100 [05:05<00:09, 3.14s/it]
98%|█████████▊| 98/100 [05:08<00:06, 3.13s/it]
99%|█████████▉| 99/100 [05:11<00:03, 3.13s/it]
100%|██████████| 100/100 [05:14<00:00, 3.13s/it]
100%|██████████| 100/100 [05:14<00:00, 3.15s/it]
- final iteration number: 100
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 314.6035399045795 seconds
----------------------------------------
linear_op = WaveletN(
wavelet_name='sym8',
nb_scale=4,
n_coils=cartesian_ref_image.shape[0],
)
regularizer_op = GroupLASSO(6e-8)
reconstructor = CalibrationlessReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='analysis',
verbose=1,
)
WARNING: Making input data immutable.
Lipschitz constant is 1.1
The lipschitz constraint is satisfied
x_final, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='condatvu',
num_iterations=100,
)
image_rec = np.linalg.norm(x_final, axis=0)
recon_ssim = ssim(image_rec, image)
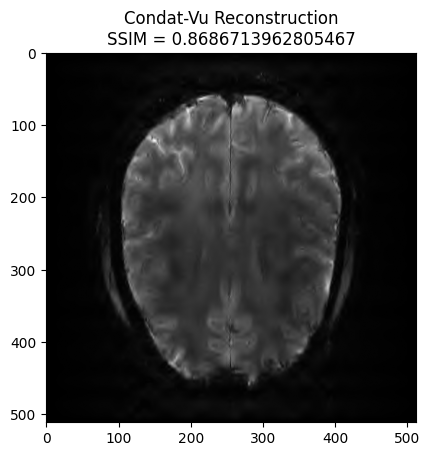
plt.imshow(np.abs(image_rec), cmap='gray')
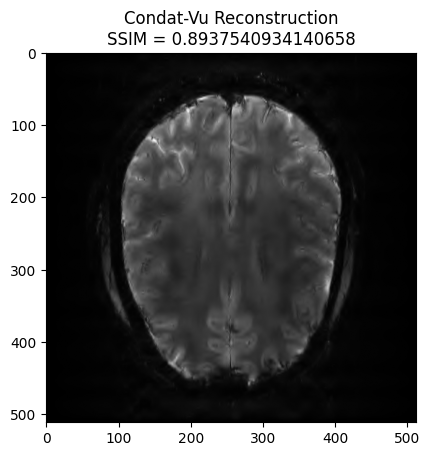
plt.title('Condat-Vu Reconstruction\nSSIM = ' + str(recon_ssim))
plt.show()
WARNING: <class 'mri.operators.linear.wavelet.WaveletN'> does not inherit an operator parent.
- mu: 6e-08
- lipschitz constant: 1.1
- tau: 0.9523809433107514
- sigma: 0.5
- rho: 1.0
- std: None
- 1/tau - sigma||L||^2 >= beta/2: True
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7718faf77370> - 4
- max iterations: 100
- number of reweights: 0
- primal variable shape: (32, 512, 512)
- dual variable shape: (32, 291721)
----------------------------------------
Starting optimization...
0%| | 0/100 [00:00<?, ?it/s]
1%| | 1/100 [00:02<03:51, 2.34s/it]
2%|▏ | 2/100 [00:04<03:48, 2.33s/it]
3%|▎ | 3/100 [00:06<03:46, 2.33s/it]
4%|▍ | 4/100 [00:09<03:43, 2.33s/it]
5%|▌ | 5/100 [00:11<03:41, 2.33s/it]
6%|▌ | 6/100 [00:13<03:38, 2.33s/it]
7%|▋ | 7/100 [00:16<03:36, 2.33s/it]
8%|▊ | 8/100 [00:18<03:34, 2.33s/it]
9%|▉ | 9/100 [00:20<03:31, 2.33s/it]
10%|█ | 10/100 [00:23<03:29, 2.33s/it]
11%|█ | 11/100 [00:25<03:26, 2.32s/it]
12%|█▏ | 12/100 [00:27<03:24, 2.33s/it]
13%|█▎ | 13/100 [00:30<03:22, 2.33s/it]
14%|█▍ | 14/100 [00:32<03:20, 2.33s/it]
15%|█▌ | 15/100 [00:34<03:17, 2.32s/it]
16%|█▌ | 16/100 [00:37<03:16, 2.33s/it]
17%|█▋ | 17/100 [00:39<03:13, 2.33s/it]
18%|█▊ | 18/100 [00:41<03:10, 2.32s/it]
19%|█▉ | 19/100 [00:44<03:07, 2.32s/it]
20%|██ | 20/100 [00:46<03:04, 2.31s/it]
21%|██ | 21/100 [00:48<03:02, 2.31s/it]
22%|██▏ | 22/100 [00:51<02:59, 2.31s/it]
23%|██▎ | 23/100 [00:53<02:57, 2.31s/it]
24%|██▍ | 24/100 [00:55<02:55, 2.30s/it]
25%|██▌ | 25/100 [00:57<02:52, 2.30s/it]
26%|██▌ | 26/100 [01:00<02:50, 2.30s/it]
27%|██▋ | 27/100 [01:02<02:47, 2.30s/it]
28%|██▊ | 28/100 [01:04<02:45, 2.30s/it]
29%|██▉ | 29/100 [01:07<02:43, 2.30s/it]
30%|███ | 30/100 [01:09<02:40, 2.30s/it]
31%|███ | 31/100 [01:11<02:38, 2.30s/it]
32%|███▏ | 32/100 [01:14<02:35, 2.29s/it]
33%|███▎ | 33/100 [01:16<02:33, 2.29s/it]
34%|███▍ | 34/100 [01:18<02:31, 2.29s/it]
35%|███▌ | 35/100 [01:20<02:29, 2.30s/it]
36%|███▌ | 36/100 [01:23<02:26, 2.29s/it]
37%|███▋ | 37/100 [01:25<02:24, 2.30s/it]
38%|███▊ | 38/100 [01:27<02:22, 2.30s/it]
39%|███▉ | 39/100 [01:30<02:19, 2.29s/it]
40%|████ | 40/100 [01:32<02:17, 2.29s/it]
41%|████ | 41/100 [01:34<02:15, 2.29s/it]
42%|████▏ | 42/100 [01:37<02:13, 2.29s/it]
43%|████▎ | 43/100 [01:39<02:10, 2.29s/it]
44%|████▍ | 44/100 [01:41<02:08, 2.29s/it]
45%|████▌ | 45/100 [01:43<02:06, 2.29s/it]
46%|████▌ | 46/100 [01:46<02:03, 2.29s/it]
47%|████▋ | 47/100 [01:48<02:01, 2.29s/it]
48%|████▊ | 48/100 [01:50<01:59, 2.29s/it]
49%|████▉ | 49/100 [01:53<01:56, 2.29s/it]
50%|█████ | 50/100 [01:55<01:54, 2.29s/it]
51%|█████ | 51/100 [01:57<01:52, 2.29s/it]
52%|█████▏ | 52/100 [01:59<01:49, 2.29s/it]
53%|█████▎ | 53/100 [02:02<01:47, 2.30s/it]
54%|█████▍ | 54/100 [02:04<01:45, 2.30s/it]
55%|█████▌ | 55/100 [02:06<01:43, 2.30s/it]
56%|█████▌ | 56/100 [02:09<01:41, 2.30s/it]
57%|█████▋ | 57/100 [02:11<01:38, 2.30s/it]
58%|█████▊ | 58/100 [02:13<01:36, 2.30s/it]
59%|█████▉ | 59/100 [02:15<01:34, 2.30s/it]
60%|██████ | 60/100 [02:18<01:31, 2.29s/it]
61%|██████ | 61/100 [02:20<01:29, 2.29s/it]
62%|██████▏ | 62/100 [02:22<01:27, 2.29s/it]
63%|██████▎ | 63/100 [02:25<01:25, 2.30s/it]
64%|██████▍ | 64/100 [02:27<01:22, 2.30s/it]
65%|██████▌ | 65/100 [02:29<01:20, 2.30s/it]
66%|██████▌ | 66/100 [02:32<01:18, 2.30s/it]
67%|██████▋ | 67/100 [02:34<01:15, 2.30s/it]
68%|██████▊ | 68/100 [02:36<01:13, 2.30s/it]
69%|██████▉ | 69/100 [02:38<01:11, 2.30s/it]
70%|███████ | 70/100 [02:41<01:08, 2.30s/it]
71%|███████ | 71/100 [02:43<01:06, 2.30s/it]
72%|███████▏ | 72/100 [02:45<01:04, 2.30s/it]
73%|███████▎ | 73/100 [02:48<01:02, 2.30s/it]
74%|███████▍ | 74/100 [02:50<00:59, 2.30s/it]
75%|███████▌ | 75/100 [02:52<00:57, 2.30s/it]
76%|███████▌ | 76/100 [02:55<00:55, 2.30s/it]
77%|███████▋ | 77/100 [02:57<00:52, 2.30s/it]
78%|███████▊ | 78/100 [02:59<00:50, 2.29s/it]
79%|███████▉ | 79/100 [03:01<00:48, 2.29s/it]
80%|████████ | 80/100 [03:04<00:45, 2.29s/it]
81%|████████ | 81/100 [03:06<00:43, 2.29s/it]
82%|████████▏ | 82/100 [03:08<00:41, 2.29s/it]
83%|████████▎ | 83/100 [03:11<00:38, 2.29s/it]
84%|████████▍ | 84/100 [03:13<00:36, 2.29s/it]
85%|████████▌ | 85/100 [03:15<00:34, 2.29s/it]
86%|████████▌ | 86/100 [03:17<00:32, 2.29s/it]
87%|████████▋ | 87/100 [03:20<00:29, 2.30s/it]
88%|████████▊ | 88/100 [03:22<00:27, 2.30s/it]
89%|████████▉ | 89/100 [03:24<00:25, 2.30s/it]
90%|█████████ | 90/100 [03:27<00:22, 2.30s/it]
91%|█████████ | 91/100 [03:29<00:20, 2.30s/it]
92%|█████████▏| 92/100 [03:31<00:18, 2.30s/it]
93%|█████████▎| 93/100 [03:34<00:16, 2.30s/it]
94%|█████████▍| 94/100 [03:36<00:13, 2.29s/it]
95%|█████████▌| 95/100 [03:38<00:11, 2.29s/it]
96%|█████████▌| 96/100 [03:40<00:09, 2.29s/it]
97%|█████████▋| 97/100 [03:43<00:06, 2.29s/it]
98%|█████████▊| 98/100 [03:45<00:04, 2.29s/it]
99%|█████████▉| 99/100 [03:47<00:02, 2.29s/it]
100%|██████████| 100/100 [03:50<00:00, 2.29s/it]
100%|██████████| 100/100 [03:50<00:00, 2.30s/it]
- final iteration number: 100
- final cost value: 1000000.0
- converged: False
Done.
Execution time: 231.339251822792 seconds
----------------------------------------
coeffs = linear_op.op(cartesian_ref_image)
regularizer_op = OWL(
alpha=1.05e-8,
beta=0,
mode='band_based',
n_coils=cartesian_ref_image.shape[0],
bands_shape=linear_op.coeffs_shape,
)
reconstructor = CalibrationlessReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='analysis',
verbose=1,
)
WARNING: Making input data immutable.
Lipschitz constant is 1.0999999344348907
The lipschitz constraint is satisfied
x_final, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_obs,
optimization_alg='condatvu',
num_iterations=100,
)
image_rec = np.linalg.norm(x_final, axis=0)
recon_ssim = ssim(image_rec, image)
plt.imshow(np.abs(image_rec), cmap='gray')
plt.title('Condat-Vu Reconstruction\nSSIM = ' + str(recon_ssim))
plt.show()
WARNING: <class 'mri.operators.linear.wavelet.WaveletN'> does not inherit an operator parent.
- mu: [<modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718f9b724a0>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718f9b72530>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fafb3e50>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718fa5e1150>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718f9b8ad40>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718f9b10940>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718f9b10850>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718f9b11540>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718f9b116c0>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718f9b10a00>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718f9b108b0>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718f9b12530>, <modopt.opt.proximity.OrderedWeightedL1Norm object at 0x7718f9b10280>]
- lipschitz constant: 1.0999999344348907
- tau: 0.9523809730454954
- sigma: 0.5
- rho: 1.0
- std: None
- 1/tau - sigma||L||^2 >= beta/2: True
- data: (512, 512)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7718faf77370> - 4
- max iterations: 100
- number of reweights: 0
- primal variable shape: (32, 512, 512)
- dual variable shape: (32, 291721)
----------------------------------------
Starting optimization...
0%| | 0/100 [00:00<?, ?it/s]
1%| | 1/100 [00:03<05:27, 3.31s/it]
2%|▏ | 2/100 [00:06<05:24, 3.31s/it]
3%|▎ | 3/100 [00:09<05:20, 3.30s/it]
4%|▍ | 4/100 [00:13<05:16, 3.30s/it]
5%|▌ | 5/100 [00:16<05:13, 3.30s/it]
6%|▌ | 6/100 [00:19<05:09, 3.29s/it]
7%|▋ | 7/100 [00:23<05:06, 3.29s/it]
8%|▊ | 8/100 [00:26<05:03, 3.30s/it]
9%|▉ | 9/100 [00:29<05:00, 3.31s/it]
10%|█ | 10/100 [00:33<04:58, 3.31s/it]
11%|█ | 11/100 [00:36<04:54, 3.31s/it]
12%|█▏ | 12/100 [00:39<04:51, 3.32s/it]
13%|█▎ | 13/100 [00:42<04:47, 3.31s/it]
14%|█▍ | 14/100 [00:46<04:44, 3.31s/it]
15%|█▌ | 15/100 [00:49<04:41, 3.31s/it]
16%|█▌ | 16/100 [00:52<04:37, 3.31s/it]
17%|█▋ | 17/100 [00:56<04:34, 3.31s/it]
18%|█▊ | 18/100 [00:59<04:31, 3.31s/it]
19%|█▉ | 19/100 [01:02<04:27, 3.30s/it]
20%|██ | 20/100 [01:06<04:22, 3.29s/it]
21%|██ | 21/100 [01:09<04:18, 3.27s/it]
22%|██▏ | 22/100 [01:12<04:16, 3.28s/it]
23%|██▎ | 23/100 [01:15<04:13, 3.29s/it]
24%|██▍ | 24/100 [01:19<04:10, 3.29s/it]
25%|██▌ | 25/100 [01:22<04:07, 3.29s/it]
26%|██▌ | 26/100 [01:25<04:03, 3.30s/it]
27%|██▋ | 27/100 [01:29<04:00, 3.30s/it]
28%|██▊ | 28/100 [01:32<03:57, 3.30s/it]
29%|██▉ | 29/100 [01:35<03:54, 3.31s/it]
30%|███ | 30/100 [01:38<03:50, 3.30s/it]
31%|███ | 31/100 [01:42<03:47, 3.30s/it]
32%|███▏ | 32/100 [01:45<03:44, 3.30s/it]
33%|███▎ | 33/100 [01:48<03:41, 3.30s/it]
34%|███▍ | 34/100 [01:52<03:37, 3.30s/it]
35%|███▌ | 35/100 [01:55<03:34, 3.30s/it]
36%|███▌ | 36/100 [01:58<03:31, 3.30s/it]
37%|███▋ | 37/100 [02:02<03:27, 3.30s/it]
38%|███▊ | 38/100 [02:05<03:24, 3.30s/it]
39%|███▉ | 39/100 [02:08<03:21, 3.30s/it]
40%|████ | 40/100 [02:12<03:18, 3.30s/it]
41%|████ | 41/100 [02:15<03:14, 3.30s/it]
42%|████▏ | 42/100 [02:18<03:11, 3.30s/it]
43%|████▎ | 43/100 [02:21<03:08, 3.30s/it]
44%|████▍ | 44/100 [02:25<03:05, 3.31s/it]
45%|████▌ | 45/100 [02:28<03:01, 3.31s/it]
46%|████▌ | 46/100 [02:31<02:58, 3.30s/it]
47%|████▋ | 47/100 [02:35<02:55, 3.31s/it]
48%|████▊ | 48/100 [02:38<02:51, 3.30s/it]
49%|████▉ | 49/100 [02:41<02:48, 3.30s/it]
50%|█████ | 50/100 [02:45<02:45, 3.31s/it]
51%|█████ | 51/100 [02:48<02:41, 3.30s/it]
52%|█████▏ | 52/100 [02:51<02:38, 3.30s/it]
53%|█████▎ | 53/100 [02:54<02:35, 3.30s/it]
54%|█████▍ | 54/100 [02:58<02:32, 3.31s/it]
55%|█████▌ | 55/100 [03:01<02:28, 3.30s/it]
56%|█████▌ | 56/100 [03:04<02:25, 3.30s/it]
57%|█████▋ | 57/100 [03:08<02:22, 3.31s/it]
58%|█████▊ | 58/100 [03:11<02:18, 3.30s/it]
59%|█████▉ | 59/100 [03:14<02:15, 3.30s/it]
60%|██████ | 60/100 [03:18<02:12, 3.30s/it]
61%|██████ | 61/100 [03:21<02:08, 3.30s/it]
62%|██████▏ | 62/100 [03:24<02:05, 3.30s/it]
63%|██████▎ | 63/100 [03:27<02:02, 3.30s/it]
64%|██████▍ | 64/100 [03:31<01:58, 3.30s/it]
65%|██████▌ | 65/100 [03:34<01:55, 3.30s/it]
66%|██████▌ | 66/100 [03:37<01:52, 3.30s/it]
67%|██████▋ | 67/100 [03:41<01:48, 3.30s/it]
68%|██████▊ | 68/100 [03:44<01:45, 3.30s/it]
69%|██████▉ | 69/100 [03:47<01:42, 3.29s/it]
70%|███████ | 70/100 [03:51<01:38, 3.29s/it]
71%|███████ | 71/100 [03:54<01:35, 3.29s/it]
72%|███████▏ | 72/100 [03:57<01:32, 3.29s/it]
73%|███████▎ | 73/100 [04:00<01:28, 3.29s/it]
74%|███████▍ | 74/100 [04:04<01:25, 3.29s/it]
75%|███████▌ | 75/100 [04:07<01:22, 3.29s/it]
76%|███████▌ | 76/100 [04:10<01:19, 3.30s/it]
77%|███████▋ | 77/100 [04:14<01:15, 3.30s/it]
78%|███████▊ | 78/100 [04:17<01:12, 3.30s/it]
79%|███████▉ | 79/100 [04:20<01:09, 3.30s/it]
80%|████████ | 80/100 [04:23<01:05, 3.30s/it]
81%|████████ | 81/100 [04:27<01:02, 3.30s/it]
82%|████████▏ | 82/100 [04:30<00:59, 3.30s/it]
83%|████████▎ | 83/100 [04:33<00:56, 3.30s/it]
84%|████████▍ | 84/100 [04:37<00:52, 3.31s/it]
85%|████████▌ | 85/100 [04:40<00:49, 3.31s/it]
86%|████████▌ | 86/100 [04:43<00:46, 3.31s/it]
87%|████████▋ | 87/100 [04:47<00:42, 3.31s/it]
88%|████████▊ | 88/100 [04:50<00:39, 3.30s/it]
89%|████████▉ | 89/100 [04:53<00:36, 3.30s/it]
90%|█████████ | 90/100 [04:57<00:33, 3.30s/it]
91%|█████████ | 91/100 [05:00<00:29, 3.30s/it]
92%|█████████▏| 92/100 [05:03<00:26, 3.30s/it]
93%|█████████▎| 93/100 [05:06<00:23, 3.30s/it]
94%|█████████▍| 94/100 [05:10<00:19, 3.30s/it]
95%|█████████▌| 95/100 [05:13<00:16, 3.29s/it]
96%|█████████▌| 96/100 [05:16<00:13, 3.29s/it]
97%|█████████▋| 97/100 [05:20<00:09, 3.29s/it]
98%|█████████▊| 98/100 [05:23<00:06, 3.29s/it]
99%|█████████▉| 99/100 [05:26<00:03, 3.29s/it]
100%|██████████| 100/100 [05:29<00:00, 3.29s/it]
100%|██████████| 100/100 [05:29<00:00, 3.30s/it]
- final iteration number: 100
- final cost value: 1000000.0
- converged: False
Done.
Execution time: 331.15869130101055 seconds
----------------------------------------