9. Iterative CS-based MR image reconstruction from Cartesian data#
In this tutorial we will reconstruct an MR image from Cartesian under-sampled kspace measurements.
We use the toy datasets available in pysap, more specifically a 2D brain slice and the cartesian acquisition scheme. We compare zero-order image reconstruction with Compressed sensing reconstructions (analysis vs synthesis formulation) using the FISTA algorithm for the synthesis formulation and the Condat-Vu algorithm for the analysis formulation.Sparsity will be promoted in the wavelet domain, using either Symmlet-8 (analysis and synthesis) or undecimated bi-orthogonal wavelets (analysis only).
We remind that the synthesis formulation reads (minimization in the sparsifying domain):
and the image solution is given by \(\widehat{x} = \Psi^*\widehat{z}\). For an orthonormal wavelet transform, we have \(n_\Psi=n\) while for a frame we may have \(n_\Psi > n\).
while the analysis formulation consists in minimizing the following cost function (min. in the image domain):
Author: Chaithya G R & Philippe Ciuciu
Date: 01/06/2021
Update: 04/02/2025
Target: ATSI MSc students, Paris-Saclay University
#DISPLAY BRAIN PHANTOM
%matplotlib inline
import numpy as np
from mri.operators.utils import convert_mask_to_locations
from mri.reconstructors import SingleChannelReconstructor
from mri.operators import FFT, WaveletN, WaveletUD2
import os.path as op
import os
import math ; import cmath
import matplotlib.pyplot as plt
import sys
from modopt.math.metrics import ssim
from modopt.opt.proximity import SparseThreshold
from modopt.opt.linear import Identity
from skimage import data, io, filters
import pywt as pw
import matplotlib.pyplot as plt
import brainweb_dl as bwdl
plt.rcParams["image.origin"]="lower"
plt.rcParams["image.cmap"]='Greys_r'
mri_img = bwdl.get_mri(4, "T1")[70, ...].astype(np.float32)
#mri_img = bwdl.get_mri(4, "T2")[120, ...].astype(np.float32)
print(mri_img.shape)
img_size = mri_img.shape[0]
plt.figure()
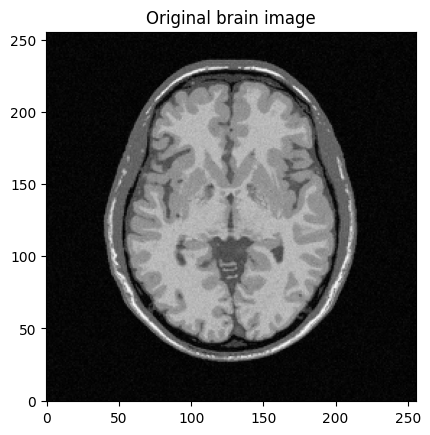
plt.imshow(abs(mri_img))
plt.title("Original brain image")
plt.show()
/volatile/github-ci-mind-inria/gpu_mind_runner/_work/mri-acq-recon-book/mri-acq-recon-book/venv/lib/python3.10/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html
from .autonotebook import tqdm as notebook_tqdm
(256, 256)
#image = get_sample_data('2d-mri')
# Obtain K-Space Cartesian Mask
#mask = get_sample_data("cartesian-mri-mask")
image = mri_img
from mrinufft.trajectories.tools import get_random_loc_1d
phase_encoding_locs = get_random_loc_1d(image.shape[0], accel=8, center_prop=0.1, pdf='gaussian')
print(phase_encoding_locs, min(phase_encoding_locs), max(phase_encoding_locs))
phase_encoding_locs = ((phase_encoding_locs +0.5) * image.shape[0]).astype(int)
mask = np.zeros(image.shape, dtype=bool)
mask[phase_encoding_locs] = 1
[ 0. 0.00390625 -0.00390625 0.0078125 -0.0078125 0.01171875
-0.01171875 0.015625 -0.015625 0.01953125 -0.01953125 0.0234375
-0.0234375 0.02734375 -0.02734375 0.03125 -0.03125 0.03515625
-0.03515625 0.0390625 -0.0390625 0.04296875 -0.04296875 0.046875
-0.046875 0.05859375 -0.05078125 0.09765625 -0.0546875 0.1015625
-0.06640625 0.11328125 -0.078125 0.125 -0.0859375 0.1875
-0.08984375 0.25390625 -0.12109375 0.2578125 -0.125 0.28515625
-0.12890625 0.3359375 -0.13671875 0.359375 -0.1484375 -0.15234375
-0.1640625 -0.17578125 -0.203125 -0.20703125 -0.2265625 ] -0.2265625 0.359375
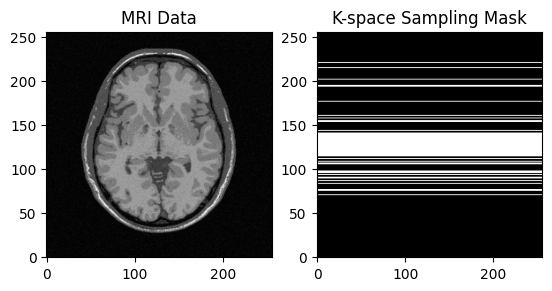
plt.subplot(1, 2, 1)
plt.imshow(np.abs(image), cmap='gray')
plt.title("MRI Data")
plt.subplot(1, 2, 2)
plt.imshow(mask, cmap='gray')
plt.title("K-space Sampling Mask")
plt.show()
Generate the kspace#
From the 2D brain slice and the acquisition mask, we retrospectively undersample the k-space using a cartesian acquisition mask. We then reconstruct the zero order solution as a baseline
Get the locations of the kspace samples
# Get the locations of the kspace samples
kspace_loc = convert_mask_to_locations(mask)
# Generate the subsampled kspace
fourier_op = FFT(samples=kspace_loc, shape=image.shape)
kspace_data = fourier_op.op(image)
Zero order solution
zero_soln = fourier_op.adj_op(kspace_data)
base_ssim = ssim(zero_soln, image)
plt.imshow(np.abs(zero_soln), cmap='gray')
plt.title('Zero Order Solution : SSIM = ' + str(np.around(base_ssim, 3)))
plt.show()
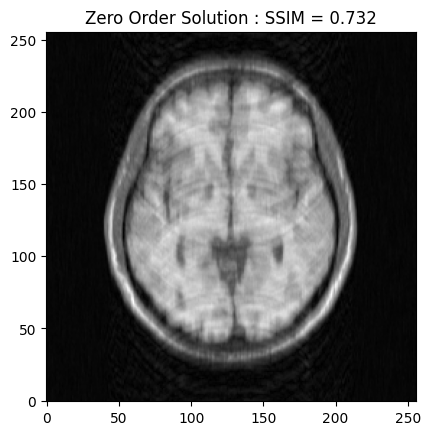
Synthesis formulation: FISTA vs POGM optimization#
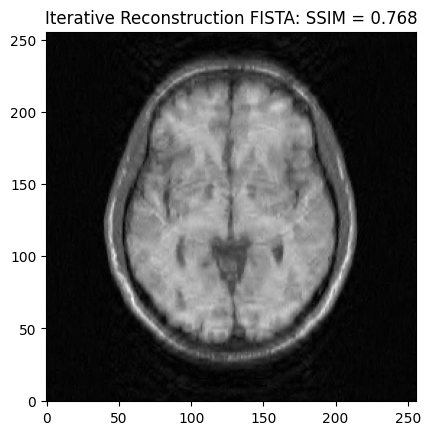
We now want to refine the zero-order solution using compressed sensing reconstruction. Here we adopt the synthesis formulation based on the FISTA algorithm. The cost function is set to Proximity Cost + Gradient Cost
# Setup the operators
linear_op = WaveletN(wavelet_name="sym8", nb_scales=4)
regularizer_op = SparseThreshold(Identity(), 0.1, thresh_type="soft")
# Setup Reconstructor
reconstructor = SingleChannelReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='synthesis',
verbose=1,
)
WARNING: Making input data immutable.
Lipschitz constant is 1.0999999483256016
The lipschitz constraint is satisfied
image_rec, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_data,
optimization_alg='fista',
num_iterations=200,
)
recon_ssim = ssim(image_rec, image)
plt.imshow(np.abs(image_rec), cmap='gray')
plt.title('Iterative Reconstruction FISTA: SSIM = ' + str(np.around(recon_ssim, 3)))
plt.show()
WARNING: Making input data immutable.
- mu: 0.1
- lipschitz constant: 1.0999999483256016
- data: (256, 256)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7ccac2b87940> - 4
- max iterations: 200
- image variable shape: (256, 256)
- alpha variable shape: (81225,)
----------------------------------------
Starting optimization...
0%| | 0/200 [00:00<?, ?it/s]
2%|▏ | 4/200 [00:00<00:05, 34.60it/s]
4%|▍ | 9/200 [00:00<00:04, 41.17it/s]
7%|▋ | 14/200 [00:00<00:04, 44.77it/s]
10%|▉ | 19/200 [00:00<00:03, 46.53it/s]
12%|█▏ | 24/200 [00:00<00:03, 47.71it/s]
14%|█▍ | 29/200 [00:00<00:03, 48.25it/s]
17%|█▋ | 34/200 [00:00<00:03, 48.75it/s]
20%|█▉ | 39/200 [00:00<00:03, 48.95it/s]
22%|██▏ | 44/200 [00:00<00:03, 49.25it/s]
24%|██▍ | 49/200 [00:01<00:03, 49.37it/s]
27%|██▋ | 54/200 [00:01<00:02, 49.37it/s]
30%|██▉ | 59/200 [00:01<00:02, 48.09it/s]
32%|███▏ | 64/200 [00:01<00:02, 48.55it/s]
34%|███▍ | 69/200 [00:01<00:02, 48.80it/s]
37%|███▋ | 74/200 [00:01<00:02, 47.66it/s]
40%|███▉ | 79/200 [00:01<00:02, 47.02it/s]
42%|████▏ | 84/200 [00:01<00:02, 47.74it/s]
44%|████▍ | 89/200 [00:01<00:02, 47.96it/s]
47%|████▋ | 94/200 [00:01<00:02, 48.21it/s]
50%|████▉ | 99/200 [00:02<00:02, 48.37it/s]
52%|█████▏ | 104/200 [00:02<00:01, 48.67it/s]
55%|█████▍ | 109/200 [00:02<00:01, 48.67it/s]
57%|█████▋ | 114/200 [00:02<00:01, 48.51it/s]
60%|█████▉ | 119/200 [00:02<00:01, 46.75it/s]
62%|██████▎ | 125/200 [00:02<00:01, 48.01it/s]
66%|██████▌ | 131/200 [00:02<00:01, 48.90it/s]
68%|██████▊ | 137/200 [00:02<00:01, 49.40it/s]
72%|███████▏ | 143/200 [00:02<00:01, 49.70it/s]
74%|███████▍ | 148/200 [00:03<00:01, 49.68it/s]
76%|███████▋ | 153/200 [00:03<00:00, 49.64it/s]
80%|███████▉ | 159/200 [00:03<00:00, 50.02it/s]
82%|████████▎ | 165/200 [00:03<00:00, 50.21it/s]
86%|████████▌ | 171/200 [00:03<00:00, 50.20it/s]
88%|████████▊ | 177/200 [00:03<00:00, 50.34it/s]
92%|█████████▏| 183/200 [00:03<00:00, 50.41it/s]
94%|█████████▍| 189/200 [00:03<00:00, 50.39it/s]
98%|█████████▊| 195/200 [00:04<00:00, 50.43it/s]
100%|██████████| 200/200 [00:04<00:00, 48.74it/s]
- final iteration number: 200
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 4.111707866191864 seconds
----------------------------------------
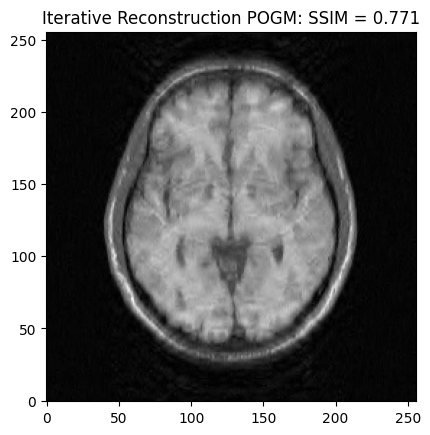
POGM optimization#
image_rec2, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_data,
optimization_alg='pogm',
num_iterations=200,
)
recon2_ssim = ssim(image_rec2, image)
plt.imshow(np.abs(image_rec2), cmap='gray')
plt.title('Iterative Reconstruction POGM: SSIM = ' + str(np.around(recon2_ssim, 3)))
plt.show()
- mu: 0.1
- lipschitz constant: 1.0999999483256016
- data: (256, 256)
- wavelet: <mri.operators.linear.wavelet.WaveletN object at 0x7ccac2b87940> - 4
- max iterations: 200
- image variable shape: (1, 256, 256)
----------------------------------------
Starting optimization...
0%| | 0/200 [00:00<?, ?it/s]
2%|▏ | 4/200 [00:00<00:05, 34.05it/s]
4%|▍ | 9/200 [00:00<00:04, 40.98it/s]
8%|▊ | 15/200 [00:00<00:04, 43.36it/s]
10%|█ | 20/200 [00:00<00:04, 37.57it/s]
12%|█▏ | 24/200 [00:00<00:05, 34.49it/s]
14%|█▍ | 28/200 [00:00<00:05, 32.75it/s]
16%|█▌ | 32/200 [00:00<00:05, 31.69it/s]
18%|█▊ | 36/200 [00:01<00:05, 30.94it/s]
20%|██ | 40/200 [00:01<00:05, 30.36it/s]
22%|██▏ | 44/200 [00:01<00:05, 29.92it/s]
24%|██▎ | 47/200 [00:01<00:05, 29.77it/s]
25%|██▌ | 50/200 [00:01<00:05, 29.68it/s]
26%|██▋ | 53/200 [00:01<00:04, 29.53it/s]
28%|██▊ | 56/200 [00:01<00:04, 29.43it/s]
30%|██▉ | 59/200 [00:01<00:04, 29.25it/s]
31%|███ | 62/200 [00:01<00:04, 29.21it/s]
32%|███▎ | 65/200 [00:02<00:04, 29.24it/s]
34%|███▍ | 68/200 [00:02<00:04, 29.17it/s]
36%|███▌ | 71/200 [00:02<00:04, 29.14it/s]
37%|███▋ | 74/200 [00:02<00:04, 29.13it/s]
38%|███▊ | 77/200 [00:02<00:04, 29.11it/s]
40%|████ | 80/200 [00:02<00:04, 29.12it/s]
42%|████▏ | 83/200 [00:02<00:04, 29.21it/s]
43%|████▎ | 86/200 [00:02<00:03, 29.19it/s]
44%|████▍ | 89/200 [00:02<00:03, 29.16it/s]
46%|████▌ | 92/200 [00:02<00:03, 29.10it/s]
48%|████▊ | 95/200 [00:03<00:03, 29.11it/s]
49%|████▉ | 98/200 [00:03<00:03, 29.13it/s]
50%|█████ | 101/200 [00:03<00:03, 29.15it/s]
52%|█████▏ | 104/200 [00:03<00:03, 29.20it/s]
54%|█████▎ | 107/200 [00:03<00:03, 29.13it/s]
55%|█████▌ | 110/200 [00:03<00:03, 29.00it/s]
56%|█████▋ | 113/200 [00:03<00:02, 29.02it/s]
58%|█████▊ | 116/200 [00:03<00:02, 29.04it/s]
60%|█████▉ | 119/200 [00:03<00:02, 29.00it/s]
61%|██████ | 122/200 [00:04<00:02, 29.02it/s]
62%|██████▎ | 125/200 [00:04<00:02, 27.57it/s]
64%|██████▍ | 128/200 [00:04<00:02, 28.02it/s]
66%|██████▌ | 131/200 [00:04<00:02, 28.48it/s]
67%|██████▋ | 134/200 [00:04<00:02, 24.40it/s]
68%|██████▊ | 137/200 [00:04<00:02, 25.68it/s]
70%|███████ | 140/200 [00:04<00:02, 26.64it/s]
72%|███████▏ | 143/200 [00:04<00:02, 27.30it/s]
73%|███████▎ | 146/200 [00:04<00:01, 27.84it/s]
74%|███████▍ | 149/200 [00:05<00:01, 28.20it/s]
76%|███████▌ | 152/200 [00:05<00:01, 28.40it/s]
78%|███████▊ | 155/200 [00:05<00:01, 28.62it/s]
79%|███████▉ | 158/200 [00:05<00:01, 28.73it/s]
80%|████████ | 161/200 [00:05<00:01, 28.91it/s]
82%|████████▏ | 164/200 [00:05<00:01, 29.00it/s]
84%|████████▎ | 167/200 [00:05<00:01, 29.08it/s]
85%|████████▌ | 170/200 [00:05<00:01, 29.12it/s]
86%|████████▋ | 173/200 [00:05<00:00, 29.14it/s]
88%|████████▊ | 176/200 [00:05<00:00, 29.17it/s]
90%|████████▉ | 179/200 [00:06<00:00, 29.24it/s]
91%|█████████ | 182/200 [00:06<00:00, 29.25it/s]
92%|█████████▎| 185/200 [00:06<00:00, 29.26it/s]
94%|█████████▍| 188/200 [00:06<00:00, 29.28it/s]
96%|█████████▌| 191/200 [00:06<00:00, 29.30it/s]
97%|█████████▋| 194/200 [00:06<00:00, 29.22it/s]
98%|█████████▊| 197/200 [00:06<00:00, 29.23it/s]
100%|██████████| 200/200 [00:06<00:00, 29.24it/s]
100%|██████████| 200/200 [00:06<00:00, 29.54it/s]
- final iteration number: 200
- final log10 cost value: 6.0
- converged: False
Done.
Execution time: 6.775225183926523 seconds
----------------------------------------
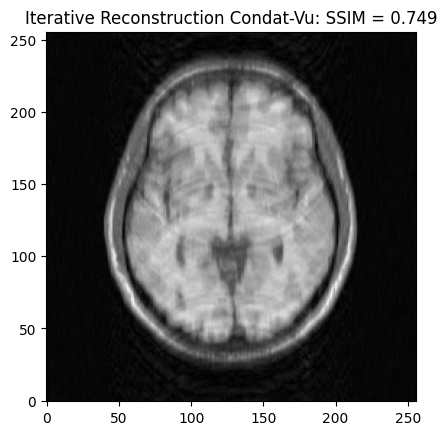
Analysis formulation: Condat-Vu reconstruction#
linear_op = WaveletUD2(
wavelet_id=24,
nb_scale=4,
)
regularizer_op = SparseThreshold(Identity(), 0.1, thresh_type="soft")
reconstructor = SingleChannelReconstructor(
fourier_op=fourier_op,
linear_op=linear_op,
regularizer_op=regularizer_op,
gradient_formulation='analysis',
verbose=1,
)
Lipschitz constant is 1.1000000547313835
The lipschitz constraint is satisfied
WARNING: Making input data immutable.
image_rec3, costs, metrics = reconstructor.reconstruct(
kspace_data=kspace_data,
optimization_alg='condatvu',
num_iterations=200,
)
recon3_ssim = ssim(image_rec3, image)
plt.imshow(np.abs(image_rec3), cmap='gray')
plt.title('Iterative Reconstruction Condat-Vu: SSIM = ' + str(np.around(recon3_ssim, 3)))
plt.show()
WARNING: <class 'mri.operators.linear.wavelet.WaveletUD2'> does not inherit an operator parent.
- mu: 0.1
- lipschitz constant: 1.1000000547313835
- tau: 0.9374654685615501
- sigma: 0.5
- rho: 1.0
- std: None
- 1/tau - sigma||L||^2 >= beta/2: True
- data: (256, 256)
- wavelet: <mri.operators.linear.wavelet.WaveletUD2 object at 0x7ccac21038e0> - 4
- max iterations: 200
- number of reweights: 0
- primal variable shape: (256, 256)
- dual variable shape: (655360,)
----------------------------------------
Starting optimization...
0%| | 0/200 [00:00<?, ?it/s]
0%| | 1/200 [00:00<01:14, 2.66it/s]
1%| | 2/200 [00:00<01:07, 2.94it/s]
2%|▏ | 3/200 [00:01<01:04, 3.05it/s]
2%|▏ | 4/200 [00:01<01:03, 3.09it/s]
2%|▎ | 5/200 [00:01<01:03, 3.05it/s]
3%|▎ | 6/200 [00:01<01:02, 3.09it/s]
4%|▎ | 7/200 [00:02<01:02, 3.06it/s]
4%|▍ | 8/200 [00:02<01:02, 3.05it/s]
4%|▍ | 9/200 [00:02<01:01, 3.09it/s]
5%|▌ | 10/200 [00:03<01:01, 3.11it/s]
6%|▌ | 11/200 [00:03<01:01, 3.08it/s]
6%|▌ | 12/200 [00:03<01:00, 3.11it/s]
6%|▋ | 13/200 [00:04<01:00, 3.08it/s]
7%|▋ | 14/200 [00:04<01:00, 3.06it/s]
8%|▊ | 15/200 [00:04<00:59, 3.09it/s]
8%|▊ | 16/200 [00:05<00:59, 3.11it/s]
8%|▊ | 17/200 [00:05<00:59, 3.08it/s]
9%|▉ | 18/200 [00:05<00:58, 3.10it/s]
10%|▉ | 19/200 [00:06<00:58, 3.07it/s]
10%|█ | 20/200 [00:06<00:58, 3.06it/s]
10%|█ | 21/200 [00:06<00:57, 3.09it/s]
11%|█ | 22/200 [00:07<00:57, 3.10it/s]
12%|█▏ | 23/200 [00:07<00:57, 3.07it/s]
12%|█▏ | 24/200 [00:07<00:56, 3.09it/s]
12%|█▎ | 25/200 [00:08<00:57, 3.06it/s]
13%|█▎ | 26/200 [00:08<00:57, 3.05it/s]
14%|█▎ | 27/200 [00:08<00:56, 3.09it/s]
14%|█▍ | 28/200 [00:09<00:55, 3.11it/s]
14%|█▍ | 29/200 [00:09<00:55, 3.08it/s]
15%|█▌ | 30/200 [00:09<00:54, 3.10it/s]
16%|█▌ | 31/200 [00:10<00:54, 3.07it/s]
16%|█▌ | 32/200 [00:10<00:54, 3.06it/s]
16%|█▋ | 33/200 [00:10<00:54, 3.09it/s]
17%|█▋ | 34/200 [00:11<00:53, 3.11it/s]
18%|█▊ | 35/200 [00:11<00:53, 3.08it/s]
18%|█▊ | 36/200 [00:11<00:52, 3.11it/s]
18%|█▊ | 37/200 [00:12<00:53, 3.07it/s]
19%|█▉ | 38/200 [00:12<00:53, 3.05it/s]
20%|█▉ | 39/200 [00:12<00:52, 3.09it/s]
20%|██ | 40/200 [00:12<00:51, 3.10it/s]
20%|██ | 41/200 [00:13<00:51, 3.07it/s]
21%|██ | 42/200 [00:13<00:51, 3.08it/s]
22%|██▏ | 43/200 [00:13<00:51, 3.06it/s]
22%|██▏ | 44/200 [00:14<00:51, 3.05it/s]
22%|██▎ | 45/200 [00:14<00:50, 3.09it/s]
23%|██▎ | 46/200 [00:14<00:49, 3.11it/s]
24%|██▎ | 47/200 [00:15<00:49, 3.08it/s]
24%|██▍ | 48/200 [00:15<00:48, 3.11it/s]
24%|██▍ | 49/200 [00:15<00:49, 3.07it/s]
25%|██▌ | 50/200 [00:16<00:49, 3.06it/s]
26%|██▌ | 51/200 [00:16<00:48, 3.09it/s]
26%|██▌ | 52/200 [00:16<00:47, 3.11it/s]
26%|██▋ | 53/200 [00:17<00:47, 3.07it/s]
27%|██▋ | 54/200 [00:17<00:47, 3.08it/s]
28%|██▊ | 55/200 [00:17<00:47, 3.06it/s]
28%|██▊ | 56/200 [00:18<00:47, 3.04it/s]
28%|██▊ | 57/200 [00:18<00:46, 3.08it/s]
29%|██▉ | 58/200 [00:18<00:45, 3.10it/s]
30%|██▉ | 59/200 [00:19<00:46, 3.06it/s]
30%|███ | 60/200 [00:19<00:45, 3.10it/s]
30%|███ | 61/200 [00:19<00:45, 3.06it/s]
31%|███ | 62/200 [00:20<00:45, 3.05it/s]
32%|███▏ | 63/200 [00:20<00:44, 3.08it/s]
32%|███▏ | 64/200 [00:20<00:43, 3.10it/s]
32%|███▎ | 65/200 [00:21<00:44, 3.06it/s]
33%|███▎ | 66/200 [00:21<00:43, 3.08it/s]
34%|███▎ | 67/200 [00:21<00:43, 3.06it/s]
34%|███▍ | 68/200 [00:22<00:43, 3.04it/s]
34%|███▍ | 69/200 [00:22<00:42, 3.08it/s]
35%|███▌ | 70/200 [00:22<00:41, 3.11it/s]
36%|███▌ | 71/200 [00:23<00:41, 3.08it/s]
36%|███▌ | 72/200 [00:23<00:41, 3.11it/s]
36%|███▋ | 73/200 [00:23<00:41, 3.08it/s]
37%|███▋ | 74/200 [00:24<00:41, 3.06it/s]
38%|███▊ | 75/200 [00:24<00:40, 3.09it/s]
38%|███▊ | 76/200 [00:24<00:39, 3.11it/s]
38%|███▊ | 77/200 [00:25<00:39, 3.08it/s]
39%|███▉ | 78/200 [00:25<00:39, 3.11it/s]
40%|███▉ | 79/200 [00:25<00:39, 3.07it/s]
40%|████ | 80/200 [00:26<00:39, 3.05it/s]
40%|████ | 81/200 [00:26<00:38, 3.09it/s]
41%|████ | 82/200 [00:26<00:38, 3.10it/s]
42%|████▏ | 83/200 [00:26<00:38, 3.07it/s]
42%|████▏ | 84/200 [00:27<00:37, 3.09it/s]
42%|████▎ | 85/200 [00:27<00:37, 3.06it/s]
43%|████▎ | 86/200 [00:27<00:37, 3.05it/s]
44%|████▎ | 87/200 [00:28<00:36, 3.09it/s]
44%|████▍ | 88/200 [00:28<00:36, 3.11it/s]
44%|████▍ | 89/200 [00:28<00:36, 3.07it/s]
45%|████▌ | 90/200 [00:29<00:35, 3.10it/s]
46%|████▌ | 91/200 [00:29<00:35, 3.07it/s]
46%|████▌ | 92/200 [00:29<00:35, 3.05it/s]
46%|████▋ | 93/200 [00:30<00:34, 3.08it/s]
47%|████▋ | 94/200 [00:30<00:34, 3.10it/s]
48%|████▊ | 95/200 [00:30<00:34, 3.07it/s]
48%|████▊ | 96/200 [00:31<00:33, 3.09it/s]
48%|████▊ | 97/200 [00:31<00:33, 3.06it/s]
49%|████▉ | 98/200 [00:31<00:33, 3.04it/s]
50%|████▉ | 99/200 [00:32<00:32, 3.08it/s]
50%|█████ | 100/200 [00:32<00:32, 3.09it/s]
50%|█████ | 101/200 [00:32<00:32, 3.06it/s]
51%|█████ | 102/200 [00:33<00:31, 3.09it/s]
52%|█████▏ | 103/200 [00:33<00:31, 3.06it/s]
52%|█████▏ | 104/200 [00:33<00:31, 3.04it/s]
52%|█████▎ | 105/200 [00:34<00:30, 3.08it/s]
53%|█████▎ | 106/200 [00:34<00:30, 3.09it/s]
54%|█████▎ | 107/200 [00:34<00:30, 3.07it/s]
54%|█████▍ | 108/200 [00:35<00:29, 3.09it/s]
55%|█████▍ | 109/200 [00:35<00:29, 3.06it/s]
55%|█████▌ | 110/200 [00:35<00:29, 3.05it/s]
56%|█████▌ | 111/200 [00:36<00:28, 3.08it/s]
56%|█████▌ | 112/200 [00:36<00:28, 3.10it/s]
56%|█████▋ | 113/200 [00:36<00:28, 3.07it/s]
57%|█████▋ | 114/200 [00:37<00:27, 3.10it/s]
57%|█████▊ | 115/200 [00:37<00:27, 3.07it/s]
58%|█████▊ | 116/200 [00:37<00:27, 3.05it/s]
58%|█████▊ | 117/200 [00:38<00:26, 3.09it/s]
59%|█████▉ | 118/200 [00:38<00:26, 3.11it/s]
60%|█████▉ | 119/200 [00:38<00:26, 3.08it/s]
60%|██████ | 120/200 [00:38<00:25, 3.10it/s]
60%|██████ | 121/200 [00:39<00:25, 3.07it/s]
61%|██████ | 122/200 [00:39<00:25, 3.06it/s]
62%|██████▏ | 123/200 [00:39<00:24, 3.09it/s]
62%|██████▏ | 124/200 [00:40<00:24, 3.11it/s]
62%|██████▎ | 125/200 [00:40<00:24, 3.04it/s]
63%|██████▎ | 126/200 [00:40<00:24, 3.08it/s]
64%|██████▎ | 127/200 [00:41<00:23, 3.05it/s]
64%|██████▍ | 128/200 [00:41<00:23, 3.04it/s]
64%|██████▍ | 129/200 [00:41<00:23, 3.08it/s]
65%|██████▌ | 130/200 [00:42<00:22, 3.10it/s]
66%|██████▌ | 131/200 [00:42<00:22, 3.07it/s]
66%|██████▌ | 132/200 [00:42<00:21, 3.10it/s]
66%|██████▋ | 133/200 [00:43<00:21, 3.05it/s]
67%|██████▋ | 134/200 [00:43<00:21, 3.04it/s]
68%|██████▊ | 135/200 [00:43<00:21, 3.08it/s]
68%|██████▊ | 136/200 [00:44<00:20, 3.09it/s]
68%|██████▊ | 137/200 [00:44<00:20, 3.06it/s]
69%|██████▉ | 138/200 [00:44<00:20, 3.08it/s]
70%|██████▉ | 139/200 [00:45<00:20, 3.05it/s]
70%|███████ | 140/200 [00:45<00:19, 3.04it/s]
70%|███████ | 141/200 [00:45<00:19, 3.07it/s]
71%|███████ | 142/200 [00:46<00:18, 3.08it/s]
72%|███████▏ | 143/200 [00:46<00:18, 3.06it/s]
72%|███████▏ | 144/200 [00:46<00:18, 3.08it/s]
72%|███████▎ | 145/200 [00:47<00:18, 3.05it/s]
73%|███████▎ | 146/200 [00:47<00:17, 3.04it/s]
74%|███████▎ | 147/200 [00:47<00:17, 3.07it/s]
74%|███████▍ | 148/200 [00:48<00:16, 3.07it/s]
74%|███████▍ | 149/200 [00:48<00:16, 3.05it/s]
75%|███████▌ | 150/200 [00:48<00:16, 3.07it/s]
76%|███████▌ | 151/200 [00:49<00:16, 3.05it/s]
76%|███████▌ | 152/200 [00:49<00:15, 3.04it/s]
76%|███████▋ | 153/200 [00:49<00:15, 3.06it/s]
77%|███████▋ | 154/200 [00:50<00:14, 3.08it/s]
78%|███████▊ | 155/200 [00:50<00:14, 3.06it/s]
78%|███████▊ | 156/200 [00:50<00:14, 3.09it/s]
78%|███████▊ | 157/200 [00:51<00:14, 3.06it/s]
79%|███████▉ | 158/200 [00:51<00:13, 3.04it/s]
80%|███████▉ | 159/200 [00:51<00:13, 3.08it/s]
80%|████████ | 160/200 [00:52<00:12, 3.11it/s]
80%|████████ | 161/200 [00:52<00:12, 3.08it/s]
81%|████████ | 162/200 [00:52<00:12, 3.10it/s]
82%|████████▏ | 163/200 [00:53<00:12, 3.07it/s]
82%|████████▏ | 164/200 [00:53<00:11, 3.05it/s]
82%|████████▎ | 165/200 [00:53<00:11, 3.09it/s]
83%|████████▎ | 166/200 [00:53<00:10, 3.11it/s]
84%|████████▎ | 167/200 [00:54<00:10, 3.08it/s]
84%|████████▍ | 168/200 [00:54<00:10, 3.12it/s]
84%|████████▍ | 169/200 [00:54<00:10, 3.08it/s]
85%|████████▌ | 170/200 [00:55<00:09, 3.07it/s]
86%|████████▌ | 171/200 [00:55<00:09, 3.10it/s]
86%|████████▌ | 172/200 [00:55<00:08, 3.12it/s]
86%|████████▋ | 173/200 [00:56<00:08, 3.09it/s]
87%|████████▋ | 174/200 [00:56<00:08, 3.12it/s]
88%|████████▊ | 175/200 [00:56<00:08, 3.08it/s]
88%|████████▊ | 176/200 [00:57<00:07, 3.06it/s]
88%|████████▊ | 177/200 [00:57<00:07, 3.09it/s]
89%|████████▉ | 178/200 [00:57<00:07, 3.11it/s]
90%|████████▉ | 179/200 [00:58<00:06, 3.08it/s]
90%|█████████ | 180/200 [00:58<00:06, 3.11it/s]
90%|█████████ | 181/200 [00:58<00:06, 3.08it/s]
91%|█████████ | 182/200 [00:59<00:05, 3.06it/s]
92%|█████████▏| 183/200 [00:59<00:05, 3.10it/s]
92%|█████████▏| 184/200 [00:59<00:05, 3.12it/s]
92%|█████████▎| 185/200 [01:00<00:04, 3.09it/s]
93%|█████████▎| 186/200 [01:00<00:04, 3.11it/s]
94%|█████████▎| 187/200 [01:00<00:04, 3.08it/s]
94%|█████████▍| 188/200 [01:01<00:03, 3.06it/s]
94%|█████████▍| 189/200 [01:01<00:03, 3.10it/s]
95%|█████████▌| 190/200 [01:01<00:03, 3.12it/s]
96%|█████████▌| 191/200 [01:02<00:02, 3.09it/s]
96%|█████████▌| 192/200 [01:02<00:02, 3.12it/s]
96%|█████████▋| 193/200 [01:02<00:02, 3.08it/s]
97%|█████████▋| 194/200 [01:03<00:01, 3.07it/s]
98%|█████████▊| 195/200 [01:03<00:01, 3.11it/s]
98%|█████████▊| 196/200 [01:03<00:01, 3.13it/s]
98%|█████████▊| 197/200 [01:03<00:00, 3.10it/s]
99%|█████████▉| 198/200 [01:04<00:00, 3.12it/s]
100%|█████████▉| 199/200 [01:04<00:00, 3.09it/s]
100%|██████████| 200/200 [01:04<00:00, 3.08it/s]
100%|██████████| 200/200 [01:04<00:00, 3.08it/s]
- final iteration number: 200
- final cost value: 1000000.0
- converged: False
Done.
Execution time: 65.36424763966352 seconds
----------------------------------------