Support recovery on simulated data (2D)

This example shows the advantages of spatially relaxed inference when dealing with high-dimensional spatial data. To do so, we compare several statistical methods that aim at recovering the support, i.e., predictive features. Among those methods some leverage the spatial structure of the data. For more details about the inference algorithms presented in this example or about the generative process used to simulate the data, please refer to Chevalier et al. (2021) [1].

This example corresponds to the experiment described in details in Chevalier et al. (2021) [1]. Shortly, to simulate the data, we draw n_samples i.i.d Gaussian vectors of size n_features and reshape them into squares (edges are equal to n_features ** (1/2)). Then, to introduce some spatial structure, we apply a Gaussian filter that correlates features that are nearby. The 2D data are then flattened into a design matrix X to represent it as a regression setting and to ease the computation of the simulated target y (see below). Then, we construct the weight map w which has the same shape as the 2D data, as it contains four predictive regions in every corner of the square. Similarly as for the construction of X, the map w is finally flattened into a vector beta. Lastly, to derive the target y, we draw a white Gaussian noise epsilon and use a linear generative model: y = X beta + epsilon.

The results of this experiment show that the methods that leverage the spatial structure of the data are relevant. More precisely, we show that clustered inference algorithms (e.g., CluDL) and ensembled clustered inference algorithms (e.g., EnCluDL) are more powerful than the standard inference methods (see also Chevalier et al. (2021) [1]). Indeed, when the number of features is much greater than the number of samples, standard statistical methods are unlikely to recover the support. Then, the idea of clustered inference is to compress the data without breaking the spatial structure, leading to a compressed problem close to the original problem. This results in a more powerful spatially relaxed inference. Indeed, thanks to the dimension reduction the support recovery is feasible. However, due to the spatial compression, there is a limited (and quantifiable) spatial uncertainty concerning the shape of the estimated support. Finally, by considering several choices of spatial compression, ensembled clustered inference algorithms reduce significantly the spatial uncertainty compared to clustered inference algorithms which consider only one spatial compression.

References

[1] (1,2,3)

Chevalier, J. A., Nguyen, T. B., Thirion, B., & Salmon, J. (2021). Spatially relaxed inference on high-dimensional linear models. arXiv preprint arXiv:2106.02590.

import matplotlib.pyplot as plt

Imports needed for this script

import numpy as np
from sklearn.cluster import FeatureAgglomeration
from sklearn.feature_extraction import image

from hidimstat.clustered_inference import clustered_inference
from hidimstat.desparsified_lasso import desparsified_lasso
from hidimstat.ensemble_clustered_inference import ensemble_clustered_inference
from hidimstat.scenario import multivariate_simulation
from hidimstat.stat_tools import pval_from_cb, zscore_from_pval

Specific plotting functions

The functions below are used to plot the results and illustrate the concept of spatial tolerance. If you are reading this example for the first time, you can skip this section.

The following function builds a 2D map with four active regions that are enfolded by thin tolerance regions.

def weight_map_2D_extended(shape, roi_size, delta):
    """Build weight map with visible tolerance region"""

    roi_size_extended = roi_size + delta

    # Create four regions in the corners
    w = np.zeros(shape + (5,))
    w[0:roi_size, 0:roi_size, 0] = 0.5
    w[-roi_size:, -roi_size:, 1] = 0.5
    w[0:roi_size, -roi_size:, 2] = 0.5
    w[-roi_size:, 0:roi_size, 3] = 0.5
    w[0:roi_size_extended, 0:roi_size_extended, 0] += 0.5
    w[-roi_size_extended:, -roi_size_extended:, 1] += 0.5
    w[0:roi_size_extended, -roi_size_extended:, 2] += 0.5
    w[-roi_size_extended:, 0:roi_size_extended, 3] += 0.5

    # round the shape a little bit
    for i in range(roi_size_extended):
        for j in range(roi_size_extended):
            if (i - roi_size) + (j - roi_size) >= delta:
                w[i, j, 0] = 0
                w[-i - 1, -j - 1, 1] = 0
                w[i, -j - 1, 2] = 0
                w[-i - 1, j, 3] = 0

    beta_extended = w.sum(-1).ravel()

    return beta_extended

To generate a plot that exhibits the true support and the estimated supports for every method, we define the two following functions:

def add_one_subplot(ax, map, title):
    """Add one subplot into the summary plot"""

    if map is not None:
        im = ax.imshow(map)
        im.set_clim(-1, 1)
        ax.tick_params(
            axis="both",
            which="both",
            bottom=False,
            top=False,
            left=False,
            labelbottom=False,
            labelleft=False,
        )
        ax.set_title(title)
    else:
        ax.axis("off")
        ax.get_xaxis().set_visible(False)
        ax.get_yaxis().set_visible(False)


def plot(maps, titles):
    """Make a summary plot from estimated supports"""

    fig, axes = plt.subplots(3, 2, figsize=(4, 6))

    for i in range(3):
        for j in range(2):
            k = i * 2 + j
            add_one_subplot(axes[i][j], maps[k], titles[k])

    fig.tight_layout()

    plt.show()

Generating the data

After setting the simulation parameters, we run the function that generates the 2D scenario that we have briefly described in the first section of this example.

# simulation parameters
n_samples = 100
shape = (40, 40)
n_features = shape[1] * shape[0]
roi_size = 4  # size of the edge of the four predictive regions
sigma = 2.0  # noise standard deviation
smooth_X = 1.0  # level of spatial smoothing introduced by the Gaussian filter

# generating the data
X_init, y, beta, epsilon, _, _ = multivariate_simulation(
    n_samples, shape, roi_size, sigma, smooth_X, seed=1
)

Choosing inference parameters

The choice of the number of clusters depends on several parameters, such as: the structure of the data (a higher correlation between neighboring features enable a greater dimension reduction, i.e. a smaller number of clusters), the number of samples (small datasets require more dimension reduction) and the required spatial tolerance (small clusters lead to limited spatial uncertainty). Formally, “spatial tolerance” is defined by the largest distance from the true support for which the occurence of a false discovery is not statistically controlled (c.f. References). Theoretically, the spatial tolerance delta is equal to the largest cluster diameter. However this choice is conservative, notably in the case of ensembled clustered inference. For these algorithms, we recommend to take the average cluster radius. In this example, we choose n_clusters = 200, leading to a theoretical spatial tolerance delta = 6, which is still conservative (see Results).

# hyper-parameters
n_clusters = 200

# inference parameters
fwer_target = 0.1
delta = 6

# computation parameter
n_jobs = 1

Computing z-score thresholds for support estimation

Below, we translate the FWER target into z-score targets. To compute the z-score targets we also take into account for the multiple testing correction. To do so, we consider Bonferroni correction. For methods that do not reduce the feature space, the correction consists in dividing the targeted FWER target by the number of features. For methods that group features into clusters, the correction consists in dividing by the number of clusters.

# computing the z-score thresholds for feature selection
correction_no_cluster = 1.0 / n_features
correction_cluster = 1.0 / n_clusters
thr_c = zscore_from_pval((fwer_target / 2) * correction_cluster)
thr_nc = zscore_from_pval((fwer_target / 2) * correction_no_cluster)

Inference with several algorithms

First, we compute a reference map that exhibits the true support and the theoretical tolerance region.

# compute true support with visible spatial tolerance
beta_extended = weight_map_2D_extended(shape, roi_size, delta)

Now, we compute the support estimated by a high-dimensional statistical infernece method that does not leverage the data structure. This method was introduced by Javanmard, A. et al. (2014), Zhang, C. H. et al. (2014) and Van de Geer, S. et al.. (2014) (full references are available at https://mind-inria.github.io/hidimstat/). and referred to as Desparsified Lasso.

# compute desparsified lasso
beta_hat, cb_min, cb_max = desparsified_lasso(X_init, y, n_jobs=n_jobs)
pval, pval_corr, one_minus_pval, one_minus_pval_corr = pval_from_cb(cb_min, cb_max)

# compute estimated support (first method)
zscore = zscore_from_pval(pval, one_minus_pval)
selected_dl = zscore > thr_nc  # use the "no clustering threshold"

# compute estimated support (second method)
selected_dl = np.logical_or(
    pval_corr < fwer_target / 2, one_minus_pval_corr < fwer_target / 2
)

Now, we compute the support estimated using a clustered inference algorithm (c.f. References) called Clustered Desparsified Lasso (CluDL) since it uses the Desparsified Lasso technique after clustering the data.

# Define the FeatureAgglomeration object that performs the clustering.
# This object is necessary to run the current algorithm and the following one.
connectivity = image.grid_to_graph(n_x=shape[0], n_y=shape[1])
ward = FeatureAgglomeration(
    n_clusters=n_clusters, connectivity=connectivity, linkage="ward"
)

# clustered desparsified lasso (CluDL)
beta_hat, pval, pval_corr, one_minus_pval, one_minus_pval_corr = clustered_inference(
    X_init, y, ward, n_clusters
)

# compute estimated support (first method)
zscore = zscore_from_pval(pval, one_minus_pval)
selected_cdl = zscore > thr_c  # use the "clustering threshold"

# compute estimated support (second method)
selected_cdl = np.logical_or(
    pval_corr < fwer_target / 2, one_minus_pval_corr < fwer_target / 2
)

Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 0

Finally, we compute the support estimated by an ensembled clustered inference algorithm (c.f. References). This algorithm is called Ensemble of Clustered Desparsified Lasso (EnCluDL) since it runs several CluDL algorithms with different clustering choices. The different CluDL solutions are then aggregated into one.

# ensemble of clustered desparsified lasso (EnCluDL)
beta_hat, pval, pval_corr, one_minus_pval, one_minus_pval_corr = (
    ensemble_clustered_inference(X_init, y, ward, n_clusters, train_size=0.3)
)

# compute estimated support
selected_ecdl = np.logical_or(
    pval_corr < fwer_target / 2, one_minus_pval_corr < fwer_target / 2
)

Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 0
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 1
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 2
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 3
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 4
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 5
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 6
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 7
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 8
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 9
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 10
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 11
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 12
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 13
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 14
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 15
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 16
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 17
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 18
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 19
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 20
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 21
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 22
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 23
Clustered inference: n_clusters = 200, inference method = desparsified-lasso, seed = 24

Results

Now we plot the true support, the theoretical tolerance regions and the estimated supports for every method.

maps = []
titles = []

maps.append(np.reshape(beta, shape))
titles.append("True weights")

maps.append(np.reshape(beta_extended, shape))
titles.append("True weights \nwith tolerance")

maps.append(np.reshape(selected_dl, shape))
titles.append("Desparsified Lasso")

maps.append(None)
titles.append(None)

maps.append(np.reshape(selected_cdl, shape))
titles.append("CluDL")

maps.append(np.reshape(selected_ecdl, shape))
titles.append("EnCluDL")

plot(maps, titles)

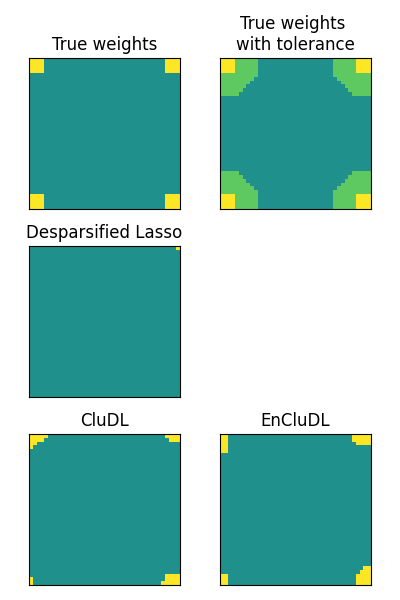
Analysis of the results

As argued in the first section of this example, standard inference methods that do not compress the problem dramatically lack power. The support estimated from CluDL provides a more reasonable solution since we recover the four regions. However the shape of the estimated support is a bit rough (as it is bound to a sub-optimal clustering). Finally, the solution provided by EnCluDL is more accurate since the shape of the estimated support is closer to the true support. Also, one can note that the theoretical spatial tolerance is quite conservative. In practice, Type-1 Error guarantees seem to hold for a lower spatial tolerance. This is an additional benefit of clustering randomization.

Estimated memory usage: 705 MB