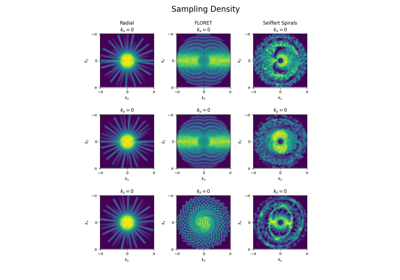
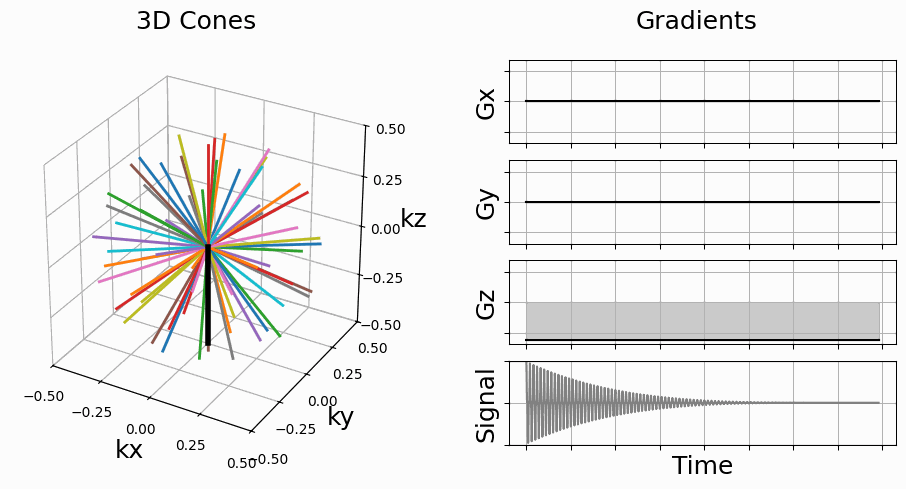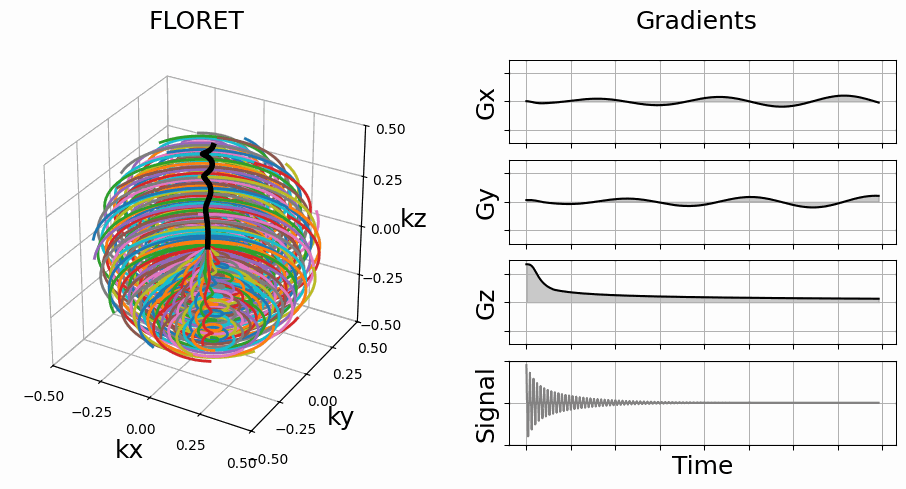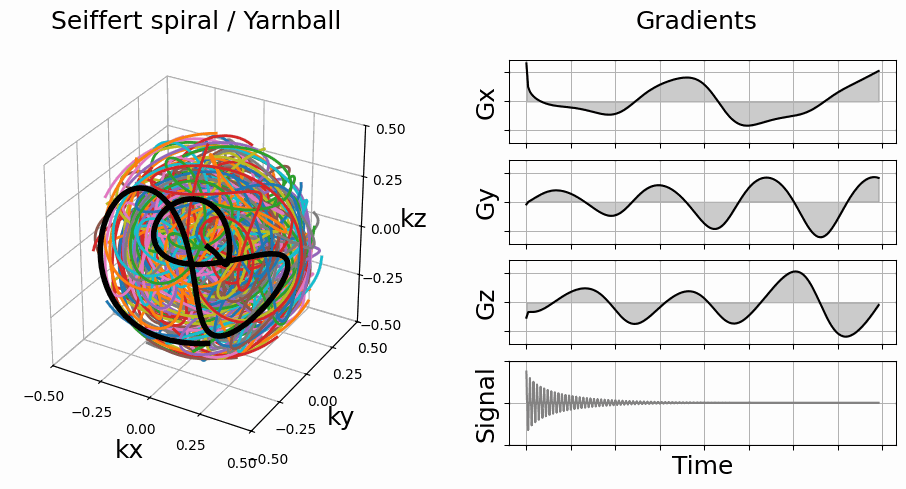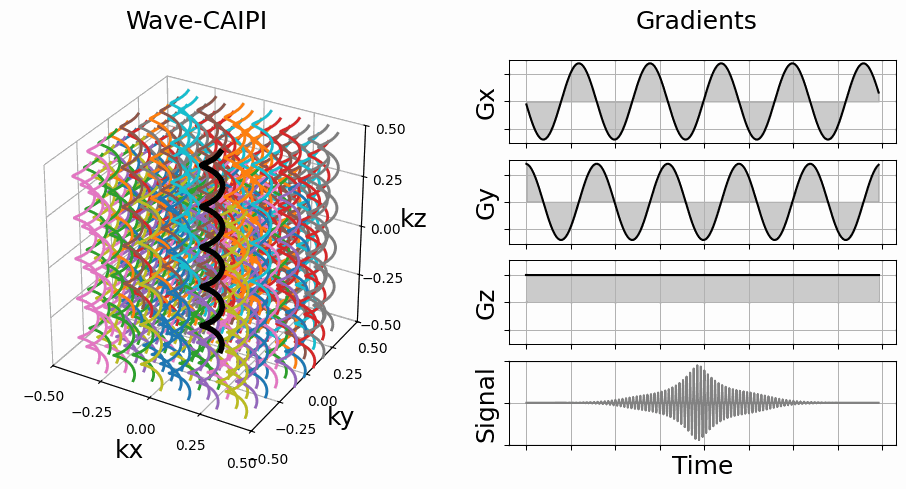
initialize_3D_seiffert_spiral

initialize_3D_seiffert_spiral#

mrinufft.trajectories.trajectory3D.initialize_3D_seiffert_spiral(Nc, Ns, curve_index=0.2, nb_revolutions=1, axis_tilt='golden', spiral_tilt='golden', in_out=False)[source]#

Initialize 3D trajectories with modulated Seiffert spirals.

Initially introduced in [SMR18], but also proposed later as “Yarnball” in [SB21] as a nod to [IN95]. The implementation is based on work from [Er00] and [Br09], using Jacobi elliptic functions rather than auxiliary theta functions.

Parameters:

  • Nc (int) – Number of shots

  • Ns (int) – Number of samples per shot

  • curve_index (float) – Index controlling curve from 0 (flat) to 1 (curvy), by default 0.3

  • nb_revolutions (float) – Number of revolutions, i.e. times the polar angle of the curves passes through 0, by default 1

  • axis_tilt (str, float, optional) – Angle between shots over a precession around the z-axis, by default “golden”

  • spiral_tilt (str, float, optional) – Angle of the spiral within its own axis defined from center to its outermost point, by default “golden”

  • in_out (bool) – Whether the curves are going in-and-out or start from the center, by default False

Returns:

3D Seiffert spiral trajectory

Return type:

array_like

References

[IN95]

Irarrazabal, Pablo, and Dwight G. Nishimura. “Fast three dimensional magnetic resonance imaging.” Magnetic Resonance in Medicine 33, no. 5 (1995): 656-662.

[Er00]

Erdös, Paul. “Spiraling the earth with C. G. J. jacobi.” American Journal of Physics 68, no. 10 (2000): 888-895.

[Br09]

Brizard, Alain J. “A primer on elliptic functions with applications in classical mechanics.” European journal of physics 30, no. 4 (2009): 729.

[SMR18]

Speidel, Tobias, Patrick Metze, and Volker Rasche. “Efficient 3D Low-Discrepancy k-Space Sampling Using Highly Adaptable Seiffert Spirals.” IEEE Transactions on Medical Imaging 38, no. 8 (2018): 1833-1840.

[SB21]

Stobbe, Robert W., and Christian Beaulieu. “Three‐dimensional Yarnball k‐space acquisition for accelerated MRI.” Magnetic Resonance in Medicine 85, no. 4 (2021): 1840-1854.