Note
Go to the end to download the full example code. or to run this example in your browser via Binder
Learning sampling pattern with decimation#
An example using PyTorch to showcase learning k-space sampling patterns with decimation.
This example showcases the auto-differentiation capabilities of the NUFFT operator with respect to the k-space trajectory in MRI-nufft.
Hereafter we learn the k-space sample locations \(\mathbf{K}\) using the following cost function:
where \(\mathcal{F}_\mathbf{K}\) is the forward NUFFT operator, \(D_\mathbf{K}\) is the density compensator for trajectory \(\mathbf{K}\), and \(\mathbf{x}\) is the MR image which is also the target image to be reconstructed.
Additionally, in order to converge faster, we also learn the trajectory in a multi-resolution fashion. This is done by first optimizing x8 times decimated trajectory locations, called control points. After a fixed number of iterations (5 in this example), these control points are upscaled by a factor of 2. Note that the NUFFT operator always holds linearly interpolated version of the control points as k-space sampling trajectory.
Note
This example can run on a binder instance as it is purely CPU based backend (finufft), and is restricted to a 2D single coil toy case.
Warning
This example only showcases the auto-differentiation capabilities, the learned sampling pattern is not scanner compliant as the gradients required to implement it violate the hardware constraints. In practice, a projection \(\Pi_\mathcal{Q}(\mathbf{K})\) onto the scanner constraints set \(\mathcal{Q}\) is recommended (see [Cha+16]). This is implemented in the proprietary SPARKLING package [Cha+22]. Users are encouraged to contact the authors if they want to use it.
import time
import brainweb_dl as bwdl
import joblib
import matplotlib.pyplot as plt
import numpy as np
import tempfile as tmp
import torch
from PIL import Image, ImageSequence
from tqdm import tqdm
from mrinufft import get_operator
from mrinufft.trajectories import initialize_2D_radial
Utils#
Model class#
Note
While we are only learning the NUFFT operator, we still need the gradient wrt_data=True to have all the gradients computed correctly. See [GRC23] for more details.
class Model(torch.nn.Module):
def __init__(
self,
inital_trajectory,
img_size=(256, 256),
start_decim=8,
interpolation_mode="linear",
):
super(Model, self).__init__()
self.control = torch.nn.Parameter(
data=torch.Tensor(inital_trajectory[:, ::start_decim]),
requires_grad=True,
)
self.current_decim = start_decim
self.interpolation_mode = interpolation_mode
sample_points = inital_trajectory.reshape(-1, inital_trajectory.shape[-1])
self.operator = get_operator("finufft", wrt_data=True, wrt_traj=True)(
sample_points,
shape=img_size,
density=True,
squeeze_dims=False,
)
self.img_size = img_size
def _interpolate(self, traj, factor=2):
"""Torch interpolate function to upsample the trajectory"""
return torch.nn.functional.interpolate(
traj.moveaxis(1, -1),
scale_factor=factor,
mode=self.interpolation_mode,
align_corners=True,
).moveaxis(-1, 1)
def get_trajectory(self):
"""Function to get trajectory, which is interpolated version of control points."""
traj = self.control.clone()
for i in range(np.log2(self.current_decim).astype(int)):
traj = self._interpolate(traj)
return traj.reshape(-1, traj.shape[-1])
def upscale(self, factor=2):
"""Upscaling the model.
In this step, the number of control points are doubled and interpolated.
"""
self.control = torch.nn.Parameter(
data=self._interpolate(self.control),
requires_grad=True,
)
self.current_decim /= factor
def forward(self, x):
traj = self.get_trajectory()
self.operator.samples = traj
# Simulate the acquisition process
kspace = self.operator.op(x)
adjoint = self.operator.adj_op(kspace).abs()
return adjoint / torch.mean(adjoint)
State plotting#
def plot_state(axs, image, traj, recon, control_points=None, loss=None, save_name=None):
axs = axs.flatten()
# Upper left reference image
axs[0].imshow(np.abs(image[0]), cmap="gray")
axs[0].axis("off")
axs[0].set_title("MR Image")
# Upper right trajectory
axs[1].scatter(*traj.T, s=0.5)
if control_points is not None:
axs[1].scatter(*control_points.T, s=1, color="r")
axs[1].legend(
["Trajectory", "Control points"], loc="right", bbox_to_anchor=(2, 0.6)
)
axs[1].grid(True)
axs[1].set_title("Trajectory")
axs[1].set_xlim(-0.5, 0.5)
axs[1].set_ylim(-0.5, 0.5)
axs[1].set_aspect("equal")
# Down left reconstructed image
axs[2].imshow(np.abs(recon[0][0].detach().cpu().numpy()), cmap="gray")
axs[2].axis("off")
axs[2].set_title("Reconstruction")
# Down right loss evolution
if loss is not None:
axs[3].plot(loss)
axs[3].set_ylim(0, None)
axs[3].grid("on")
axs[3].set_title("Loss")
plt.subplots_adjust(hspace=0.3)
# Save & close
if save_name is not None:
plt.savefig(save_name, bbox_inches="tight")
plt.close()
else:
plt.show()
Optimizer upscaling#
def upsample_optimizer(optimizer, new_optimizer, factor=2):
"""Upsample the optimizer."""
for old_group, new_group in zip(optimizer.param_groups, new_optimizer.param_groups):
for old_param, new_param in zip(old_group["params"], new_group["params"]):
# Interpolate optimizer states
if old_param in optimizer.state:
for key in optimizer.state[old_param].keys():
if isinstance(optimizer.state[old_param][key], torch.Tensor):
old_state = optimizer.state[old_param][key]
if old_state.ndim == 0:
new_state = old_state
else:
new_state = torch.nn.functional.interpolate(
old_state.moveaxis(1, -1),
scale_factor=factor,
mode="linear",
).moveaxis(-1, 1)
new_optimizer.state[new_param][key] = new_state
else:
new_optimizer.state[new_param][key] = optimizer.state[
old_param
][key]
return new_optimizer
Data preparation#
A single image to train the model over. Note that in practice we would use a whole dataset instead (e.g. fastMRI).
volume = np.flip(bwdl.get_mri(4, "T1"), axis=(0, 1, 2))
image = torch.from_numpy(volume[-80, ...].astype(np.float32))[None]
image = image / torch.mean(image)
A basic radial trajectory with an acceleration factor of 8.
AF = 8
initial_traj = initialize_2D_radial(image.shape[1] // AF, image.shape[2]).astype(
np.float32
)
Trajectory learning#
Initialisation#
model = Model(initial_traj, img_size=image.shape[1:])
model = model.eval()
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
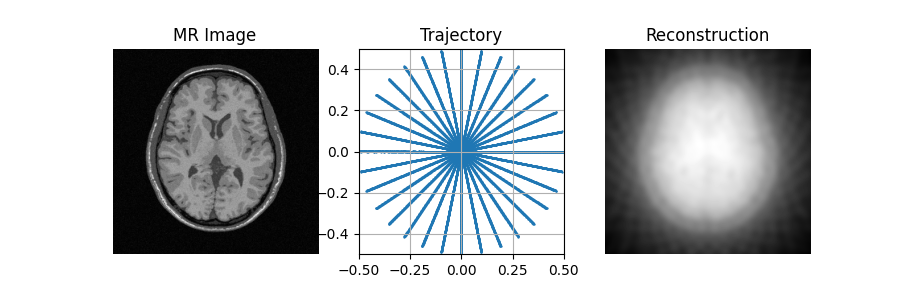
The image obtained before learning the sampling pattern is highly degraded because of the acceleration factor and simplicity of the trajectory.
initial_recons = model(image)
fig, axs = plt.subplots(1, 3, figsize=(9, 3))
plot_state(axs, image, initial_traj, initial_recons)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
Training loop#
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3)
model.train()
losses = []
image_files = []
while model.current_decim >= 1:
with tqdm(range(30), unit="steps") as tqdms:
for i in tqdms:
out = model(image)
loss = torch.nn.functional.mse_loss(out, image[None, None])
numpy_loss = (loss.detach().cpu().numpy(),)
tqdms.set_postfix({"loss": numpy_loss})
losses.append(numpy_loss)
optimizer.zero_grad()
loss.backward()
optimizer.step()
with torch.no_grad():
# Clamp the value of trajectory between [-0.5, 0.5]
for param in model.parameters():
param.clamp_(-0.5, 0.5)
# Generate images for gif
filename = f"{tmp.NamedTemporaryFile().name}.png"
plt.clf()
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
plot_state(
axs,
image,
model.get_trajectory().detach().cpu().numpy(),
out,
model.control.detach().cpu().numpy(),
losses,
save_name=filename,
)
image_files.append(filename)
if model.current_decim == 1:
break
else:
model.upscale()
optimizer = upsample_optimizer(
optimizer, torch.optim.Adam(model.parameters(), lr=1e-3)
)
0%| | 0/30 [00:00<?, ?steps/s]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
0%| | 0/30 [00:00<?, ?steps/s, loss=(array(0.54169774, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/operators/autodiff.py:98: UserWarning: Casting complex values to real discards the imaginary part (Triggered internally at /pytorch/aten/src/ATen/native/Copy.cpp:307.)
grad_traj = torch.transpose(torch.sum(grad_traj, dim=1), 0, 1).to(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
3%|▎ | 1/30 [00:01<00:42, 1.48s/steps, loss=(array(0.54169774, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
3%|▎ | 1/30 [00:02<00:42, 1.48s/steps, loss=(array(0.28933096, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
7%|▋ | 2/30 [00:02<00:38, 1.37s/steps, loss=(array(0.28933096, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
7%|▋ | 2/30 [00:03<00:38, 1.37s/steps, loss=(array(0.32130992, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
10%|█ | 3/30 [00:03<00:34, 1.28s/steps, loss=(array(0.32130992, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
10%|█ | 3/30 [00:04<00:34, 1.28s/steps, loss=(array(0.570969, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
13%|█▎ | 4/30 [00:05<00:34, 1.33s/steps, loss=(array(0.570969, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
13%|█▎ | 4/30 [00:05<00:34, 1.33s/steps, loss=(array(0.6651886, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
17%|█▋ | 5/30 [00:06<00:34, 1.37s/steps, loss=(array(0.6651886, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
17%|█▋ | 5/30 [00:07<00:34, 1.37s/steps, loss=(array(0.63610744, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
20%|██ | 6/30 [00:08<00:31, 1.33s/steps, loss=(array(0.63610744, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
20%|██ | 6/30 [00:08<00:31, 1.33s/steps, loss=(array(0.5450231, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
23%|██▎ | 7/30 [00:09<00:33, 1.45s/steps, loss=(array(0.5450231, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
23%|██▎ | 7/30 [00:10<00:33, 1.45s/steps, loss=(array(0.4305522, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
27%|██▋ | 8/30 [00:11<00:31, 1.41s/steps, loss=(array(0.4305522, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
27%|██▋ | 8/30 [00:11<00:31, 1.41s/steps, loss=(array(0.29558885, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
30%|███ | 9/30 [00:12<00:28, 1.37s/steps, loss=(array(0.29558885, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
30%|███ | 9/30 [00:13<00:28, 1.37s/steps, loss=(array(0.20528626, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
33%|███▎ | 10/30 [00:13<00:28, 1.42s/steps, loss=(array(0.20528626, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
33%|███▎ | 10/30 [00:14<00:28, 1.42s/steps, loss=(array(0.20900296, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
37%|███▋ | 11/30 [00:15<00:30, 1.59s/steps, loss=(array(0.20900296, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
37%|███▋ | 11/30 [00:16<00:30, 1.59s/steps, loss=(array(0.23116598, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
40%|████ | 12/30 [00:16<00:25, 1.43s/steps, loss=(array(0.23116598, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
40%|████ | 12/30 [00:17<00:25, 1.43s/steps, loss=(array(0.22359744, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
43%|████▎ | 13/30 [00:18<00:23, 1.37s/steps, loss=(array(0.22359744, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
43%|████▎ | 13/30 [00:18<00:23, 1.37s/steps, loss=(array(0.1994223, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
47%|████▋ | 14/30 [00:19<00:20, 1.28s/steps, loss=(array(0.1994223, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
47%|████▋ | 14/30 [00:19<00:20, 1.28s/steps, loss=(array(0.18064573, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
50%|█████ | 15/30 [00:20<00:19, 1.29s/steps, loss=(array(0.18064573, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
50%|█████ | 15/30 [00:21<00:19, 1.29s/steps, loss=(array(0.17737287, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
53%|█████▎ | 16/30 [00:21<00:18, 1.30s/steps, loss=(array(0.17737287, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
53%|█████▎ | 16/30 [00:22<00:18, 1.30s/steps, loss=(array(0.18255669, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
57%|█████▋ | 17/30 [00:23<00:16, 1.30s/steps, loss=(array(0.18255669, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
57%|█████▋ | 17/30 [00:23<00:16, 1.30s/steps, loss=(array(0.18278837, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
60%|██████ | 18/30 [00:24<00:16, 1.40s/steps, loss=(array(0.18278837, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
60%|██████ | 18/30 [00:25<00:16, 1.40s/steps, loss=(array(0.17662594, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
63%|██████▎ | 19/30 [00:26<00:15, 1.39s/steps, loss=(array(0.17662594, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
63%|██████▎ | 19/30 [00:26<00:15, 1.39s/steps, loss=(array(0.17404726, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
67%|██████▋ | 20/30 [00:27<00:14, 1.49s/steps, loss=(array(0.17404726, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
67%|██████▋ | 20/30 [00:28<00:14, 1.49s/steps, loss=(array(0.17727235, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
70%|███████ | 21/30 [00:29<00:13, 1.47s/steps, loss=(array(0.17727235, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
70%|███████ | 21/30 [00:29<00:13, 1.47s/steps, loss=(array(0.17683004, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
73%|███████▎ | 22/30 [00:30<00:11, 1.41s/steps, loss=(array(0.17683004, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
73%|███████▎ | 22/30 [00:31<00:11, 1.41s/steps, loss=(array(0.17163825, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
77%|███████▋ | 23/30 [00:32<00:10, 1.43s/steps, loss=(array(0.17163825, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
77%|███████▋ | 23/30 [00:32<00:10, 1.43s/steps, loss=(array(0.16470608, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
80%|████████ | 24/30 [00:33<00:08, 1.38s/steps, loss=(array(0.16470608, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
80%|████████ | 24/30 [00:33<00:08, 1.38s/steps, loss=(array(0.1626614, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
83%|████████▎ | 25/30 [00:34<00:06, 1.35s/steps, loss=(array(0.1626614, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
83%|████████▎ | 25/30 [00:35<00:06, 1.35s/steps, loss=(array(0.16427039, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
87%|████████▋ | 26/30 [00:35<00:05, 1.35s/steps, loss=(array(0.16427039, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
87%|████████▋ | 26/30 [00:36<00:05, 1.35s/steps, loss=(array(0.16347271, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
90%|█████████ | 27/30 [00:37<00:04, 1.39s/steps, loss=(array(0.16347271, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
90%|█████████ | 27/30 [00:37<00:04, 1.39s/steps, loss=(array(0.16347432, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
93%|█████████▎| 28/30 [00:39<00:02, 1.48s/steps, loss=(array(0.16347432, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
93%|█████████▎| 28/30 [00:40<00:02, 1.48s/steps, loss=(array(0.16488881, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
97%|█████████▋| 29/30 [00:41<00:01, 1.66s/steps, loss=(array(0.16488881, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
97%|█████████▋| 29/30 [00:42<00:01, 1.66s/steps, loss=(array(0.16544649, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
100%|██████████| 30/30 [00:42<00:00, 1.61s/steps, loss=(array(0.16544649, dtype=float32),)]
100%|██████████| 30/30 [00:42<00:00, 1.42s/steps, loss=(array(0.16544649, dtype=float32),)]
0%| | 0/30 [00:00<?, ?steps/s]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
0%| | 0/30 [00:00<?, ?steps/s, loss=(array(0.16390383, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
3%|▎ | 1/30 [00:01<00:33, 1.14s/steps, loss=(array(0.16390383, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
3%|▎ | 1/30 [00:01<00:33, 1.14s/steps, loss=(array(0.1621668, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
7%|▋ | 2/30 [00:02<00:32, 1.15s/steps, loss=(array(0.1621668, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
7%|▋ | 2/30 [00:02<00:32, 1.15s/steps, loss=(array(0.1556435, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
10%|█ | 3/30 [00:03<00:31, 1.16s/steps, loss=(array(0.1556435, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
10%|█ | 3/30 [00:04<00:31, 1.16s/steps, loss=(array(0.15082106, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
13%|█▎ | 4/30 [00:04<00:33, 1.28s/steps, loss=(array(0.15082106, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
13%|█▎ | 4/30 [00:05<00:33, 1.28s/steps, loss=(array(0.148215, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
17%|█▋ | 5/30 [00:06<00:31, 1.26s/steps, loss=(array(0.148215, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
17%|█▋ | 5/30 [00:06<00:31, 1.26s/steps, loss=(array(0.14466394, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
20%|██ | 6/30 [00:07<00:30, 1.28s/steps, loss=(array(0.14466394, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
20%|██ | 6/30 [00:08<00:30, 1.28s/steps, loss=(array(0.14311664, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
23%|██▎ | 7/30 [00:08<00:30, 1.31s/steps, loss=(array(0.14311664, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
23%|██▎ | 7/30 [00:09<00:30, 1.31s/steps, loss=(array(0.14056465, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
27%|██▋ | 8/30 [00:10<00:31, 1.42s/steps, loss=(array(0.14056465, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
27%|██▋ | 8/30 [00:11<00:31, 1.42s/steps, loss=(array(0.13835092, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
30%|███ | 9/30 [00:11<00:28, 1.38s/steps, loss=(array(0.13835092, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
30%|███ | 9/30 [00:12<00:28, 1.38s/steps, loss=(array(0.1374428, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
33%|███▎ | 10/30 [00:12<00:26, 1.32s/steps, loss=(array(0.1374428, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
33%|███▎ | 10/30 [00:13<00:26, 1.32s/steps, loss=(array(0.1371926, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
37%|███▋ | 11/30 [00:14<00:26, 1.42s/steps, loss=(array(0.1371926, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
37%|███▋ | 11/30 [00:15<00:26, 1.42s/steps, loss=(array(0.13627982, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
40%|████ | 12/30 [00:15<00:24, 1.34s/steps, loss=(array(0.13627982, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
40%|████ | 12/30 [00:16<00:24, 1.34s/steps, loss=(array(0.13499919, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
43%|████▎ | 13/30 [00:17<00:22, 1.31s/steps, loss=(array(0.13499919, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
43%|████▎ | 13/30 [00:17<00:22, 1.31s/steps, loss=(array(0.13574606, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
47%|████▋ | 14/30 [00:18<00:20, 1.28s/steps, loss=(array(0.13574606, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
47%|████▋ | 14/30 [00:18<00:20, 1.28s/steps, loss=(array(0.13570088, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
50%|█████ | 15/30 [00:19<00:18, 1.23s/steps, loss=(array(0.13570088, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
50%|█████ | 15/30 [00:19<00:18, 1.23s/steps, loss=(array(0.13444902, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
53%|█████▎ | 16/30 [00:20<00:17, 1.24s/steps, loss=(array(0.13444902, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
53%|█████▎ | 16/30 [00:21<00:17, 1.24s/steps, loss=(array(0.13302356, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
57%|█████▋ | 17/30 [00:21<00:16, 1.28s/steps, loss=(array(0.13302356, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
57%|█████▋ | 17/30 [00:22<00:16, 1.28s/steps, loss=(array(0.13213581, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
60%|██████ | 18/30 [00:22<00:14, 1.18s/steps, loss=(array(0.13213581, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
60%|██████ | 18/30 [00:23<00:14, 1.18s/steps, loss=(array(0.13094926, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
63%|██████▎ | 19/30 [00:24<00:14, 1.31s/steps, loss=(array(0.13094926, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
63%|██████▎ | 19/30 [00:25<00:14, 1.31s/steps, loss=(array(0.1295346, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
67%|██████▋ | 20/30 [00:25<00:13, 1.31s/steps, loss=(array(0.1295346, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
67%|██████▋ | 20/30 [00:26<00:13, 1.31s/steps, loss=(array(0.12891212, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
70%|███████ | 21/30 [00:27<00:11, 1.28s/steps, loss=(array(0.12891212, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
70%|███████ | 21/30 [00:27<00:11, 1.28s/steps, loss=(array(0.12838626, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
73%|███████▎ | 22/30 [00:28<00:10, 1.33s/steps, loss=(array(0.12838626, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
73%|███████▎ | 22/30 [00:28<00:10, 1.33s/steps, loss=(array(0.12780203, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
77%|███████▋ | 23/30 [00:29<00:09, 1.30s/steps, loss=(array(0.12780203, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
77%|███████▋ | 23/30 [00:30<00:09, 1.30s/steps, loss=(array(0.12699284, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
80%|████████ | 24/30 [00:31<00:08, 1.38s/steps, loss=(array(0.12699284, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
80%|████████ | 24/30 [00:31<00:08, 1.38s/steps, loss=(array(0.12666637, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
83%|████████▎ | 25/30 [00:32<00:06, 1.33s/steps, loss=(array(0.12666637, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
83%|████████▎ | 25/30 [00:33<00:06, 1.33s/steps, loss=(array(0.12594077, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
87%|████████▋ | 26/30 [00:33<00:05, 1.30s/steps, loss=(array(0.12594077, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
87%|████████▋ | 26/30 [00:34<00:05, 1.30s/steps, loss=(array(0.12517552, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
90%|█████████ | 27/30 [00:34<00:03, 1.28s/steps, loss=(array(0.12517552, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
90%|█████████ | 27/30 [00:35<00:03, 1.28s/steps, loss=(array(0.1246697, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
93%|█████████▎| 28/30 [00:36<00:02, 1.25s/steps, loss=(array(0.1246697, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
93%|█████████▎| 28/30 [00:36<00:02, 1.25s/steps, loss=(array(0.12396979, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
97%|█████████▋| 29/30 [00:37<00:01, 1.21s/steps, loss=(array(0.12396979, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
97%|█████████▋| 29/30 [00:37<00:01, 1.21s/steps, loss=(array(0.12344128, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
100%|██████████| 30/30 [00:38<00:00, 1.32s/steps, loss=(array(0.12344128, dtype=float32),)]
100%|██████████| 30/30 [00:38<00:00, 1.30s/steps, loss=(array(0.12344128, dtype=float32),)]
0%| | 0/30 [00:00<?, ?steps/s]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
0%| | 0/30 [00:00<?, ?steps/s, loss=(array(0.12286855, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
3%|▎ | 1/30 [00:01<00:37, 1.30s/steps, loss=(array(0.12286855, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
3%|▎ | 1/30 [00:01<00:37, 1.30s/steps, loss=(array(0.12157726, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
7%|▋ | 2/30 [00:02<00:36, 1.30s/steps, loss=(array(0.12157726, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
7%|▋ | 2/30 [00:03<00:36, 1.30s/steps, loss=(array(0.11990298, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
10%|█ | 3/30 [00:03<00:35, 1.31s/steps, loss=(array(0.11990298, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
10%|█ | 3/30 [00:04<00:35, 1.31s/steps, loss=(array(0.11821881, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
13%|█▎ | 4/30 [00:05<00:32, 1.26s/steps, loss=(array(0.11821881, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
13%|█▎ | 4/30 [00:05<00:32, 1.26s/steps, loss=(array(0.11665191, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
17%|█▋ | 5/30 [00:06<00:30, 1.23s/steps, loss=(array(0.11665191, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
17%|█▋ | 5/30 [00:06<00:30, 1.23s/steps, loss=(array(0.11527538, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
20%|██ | 6/30 [00:07<00:30, 1.27s/steps, loss=(array(0.11527538, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
20%|██ | 6/30 [00:08<00:30, 1.27s/steps, loss=(array(0.11410134, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
23%|██▎ | 7/30 [00:08<00:29, 1.27s/steps, loss=(array(0.11410134, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
23%|██▎ | 7/30 [00:09<00:29, 1.27s/steps, loss=(array(0.11293651, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
27%|██▋ | 8/30 [00:10<00:28, 1.27s/steps, loss=(array(0.11293651, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
27%|██▋ | 8/30 [00:10<00:28, 1.27s/steps, loss=(array(0.11174488, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
30%|███ | 9/30 [00:11<00:27, 1.30s/steps, loss=(array(0.11174488, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
30%|███ | 9/30 [00:11<00:27, 1.30s/steps, loss=(array(0.11063935, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
33%|███▎ | 10/30 [00:13<00:27, 1.36s/steps, loss=(array(0.11063935, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
33%|███▎ | 10/30 [00:14<00:27, 1.36s/steps, loss=(array(0.10956445, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
37%|███▋ | 11/30 [00:15<00:31, 1.66s/steps, loss=(array(0.10956445, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
37%|███▋ | 11/30 [00:16<00:31, 1.66s/steps, loss=(array(0.10844908, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
40%|████ | 12/30 [00:17<00:29, 1.67s/steps, loss=(array(0.10844908, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
40%|████ | 12/30 [00:17<00:29, 1.67s/steps, loss=(array(0.10726884, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
43%|████▎ | 13/30 [00:18<00:27, 1.63s/steps, loss=(array(0.10726884, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
43%|████▎ | 13/30 [00:19<00:27, 1.63s/steps, loss=(array(0.10610142, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
47%|████▋ | 14/30 [00:20<00:25, 1.62s/steps, loss=(array(0.10610142, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
47%|████▋ | 14/30 [00:20<00:25, 1.62s/steps, loss=(array(0.10509175, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
50%|█████ | 15/30 [00:21<00:23, 1.58s/steps, loss=(array(0.10509175, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
50%|█████ | 15/30 [00:22<00:23, 1.58s/steps, loss=(array(0.10422537, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
53%|█████▎ | 16/30 [00:22<00:20, 1.45s/steps, loss=(array(0.10422537, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
53%|█████▎ | 16/30 [00:23<00:20, 1.45s/steps, loss=(array(0.10342838, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
57%|█████▋ | 17/30 [00:24<00:18, 1.44s/steps, loss=(array(0.10342838, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
57%|█████▋ | 17/30 [00:24<00:18, 1.44s/steps, loss=(array(0.102764, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
60%|██████ | 18/30 [00:25<00:16, 1.37s/steps, loss=(array(0.102764, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
60%|██████ | 18/30 [00:25<00:16, 1.37s/steps, loss=(array(0.10217278, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
63%|██████▎ | 19/30 [00:26<00:15, 1.37s/steps, loss=(array(0.10217278, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
63%|██████▎ | 19/30 [00:27<00:15, 1.37s/steps, loss=(array(0.1015256, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
67%|██████▋ | 20/30 [00:28<00:14, 1.42s/steps, loss=(array(0.1015256, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
67%|██████▋ | 20/30 [00:28<00:14, 1.42s/steps, loss=(array(0.1008734, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
70%|███████ | 21/30 [00:29<00:11, 1.30s/steps, loss=(array(0.1008734, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
70%|███████ | 21/30 [00:29<00:11, 1.30s/steps, loss=(array(0.1003578, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
73%|███████▎ | 22/30 [00:30<00:10, 1.34s/steps, loss=(array(0.1003578, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
73%|███████▎ | 22/30 [00:31<00:10, 1.34s/steps, loss=(array(0.09990059, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
77%|███████▋ | 23/30 [00:32<00:09, 1.34s/steps, loss=(array(0.09990059, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
77%|███████▋ | 23/30 [00:32<00:09, 1.34s/steps, loss=(array(0.0993141, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
80%|████████ | 24/30 [00:33<00:07, 1.27s/steps, loss=(array(0.0993141, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
80%|████████ | 24/30 [00:33<00:07, 1.27s/steps, loss=(array(0.09869492, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
83%|████████▎ | 25/30 [00:34<00:06, 1.25s/steps, loss=(array(0.09869492, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
83%|████████▎ | 25/30 [00:35<00:06, 1.25s/steps, loss=(array(0.09818743, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
87%|████████▋ | 26/30 [00:35<00:05, 1.25s/steps, loss=(array(0.09818743, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
87%|████████▋ | 26/30 [00:36<00:05, 1.25s/steps, loss=(array(0.09771806, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
90%|█████████ | 27/30 [00:36<00:03, 1.24s/steps, loss=(array(0.09771806, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
90%|█████████ | 27/30 [00:37<00:03, 1.24s/steps, loss=(array(0.0972435, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
93%|█████████▎| 28/30 [00:38<00:02, 1.25s/steps, loss=(array(0.0972435, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
93%|█████████▎| 28/30 [00:39<00:02, 1.25s/steps, loss=(array(0.09676144, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
97%|█████████▋| 29/30 [00:39<00:01, 1.37s/steps, loss=(array(0.09676144, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
97%|█████████▋| 29/30 [00:40<00:01, 1.37s/steps, loss=(array(0.0963394, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
100%|██████████| 30/30 [00:40<00:00, 1.27s/steps, loss=(array(0.0963394, dtype=float32),)]
100%|██████████| 30/30 [00:40<00:00, 1.36s/steps, loss=(array(0.0963394, dtype=float32),)]
0%| | 0/30 [00:00<?, ?steps/s]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
0%| | 0/30 [00:00<?, ?steps/s, loss=(array(0.09608214, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
3%|▎ | 1/30 [00:01<00:37, 1.30s/steps, loss=(array(0.09608214, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
3%|▎ | 1/30 [00:01<00:37, 1.30s/steps, loss=(array(0.09318495, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
7%|▋ | 2/30 [00:02<00:36, 1.31s/steps, loss=(array(0.09318495, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
7%|▋ | 2/30 [00:03<00:36, 1.31s/steps, loss=(array(0.09066228, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
10%|█ | 3/30 [00:04<00:41, 1.54s/steps, loss=(array(0.09066228, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
10%|█ | 3/30 [00:05<00:41, 1.54s/steps, loss=(array(0.08951312, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
13%|█▎ | 4/30 [00:06<00:41, 1.59s/steps, loss=(array(0.08951312, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
13%|█▎ | 4/30 [00:06<00:41, 1.59s/steps, loss=(array(0.08874686, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
17%|█▋ | 5/30 [00:07<00:35, 1.42s/steps, loss=(array(0.08874686, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
17%|█▋ | 5/30 [00:07<00:35, 1.42s/steps, loss=(array(0.087819, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
20%|██ | 6/30 [00:08<00:34, 1.43s/steps, loss=(array(0.087819, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
20%|██ | 6/30 [00:09<00:34, 1.43s/steps, loss=(array(0.08688375, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
23%|██▎ | 7/30 [00:10<00:33, 1.45s/steps, loss=(array(0.08688375, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
23%|██▎ | 7/30 [00:10<00:33, 1.45s/steps, loss=(array(0.08598077, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
27%|██▋ | 8/30 [00:11<00:30, 1.38s/steps, loss=(array(0.08598077, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
27%|██▋ | 8/30 [00:11<00:30, 1.38s/steps, loss=(array(0.08520594, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
30%|███ | 9/30 [00:12<00:29, 1.39s/steps, loss=(array(0.08520594, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
30%|███ | 9/30 [00:13<00:29, 1.39s/steps, loss=(array(0.08454543, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
33%|███▎ | 10/30 [00:13<00:26, 1.32s/steps, loss=(array(0.08454543, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
33%|███▎ | 10/30 [00:14<00:26, 1.32s/steps, loss=(array(0.0836559, dtype=float32),)] /volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
37%|███▋ | 11/30 [00:15<00:24, 1.29s/steps, loss=(array(0.0836559, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
37%|███▋ | 11/30 [00:15<00:24, 1.29s/steps, loss=(array(0.0825943, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
40%|████ | 12/30 [00:16<00:25, 1.41s/steps, loss=(array(0.0825943, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
40%|████ | 12/30 [00:17<00:25, 1.41s/steps, loss=(array(0.08164643, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
43%|████▎ | 13/30 [00:18<00:25, 1.47s/steps, loss=(array(0.08164643, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
43%|████▎ | 13/30 [00:19<00:25, 1.47s/steps, loss=(array(0.08091293, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
47%|████▋ | 14/30 [00:19<00:23, 1.47s/steps, loss=(array(0.08091293, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
47%|████▋ | 14/30 [00:20<00:23, 1.47s/steps, loss=(array(0.08025898, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
50%|█████ | 15/30 [00:21<00:21, 1.45s/steps, loss=(array(0.08025898, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
50%|█████ | 15/30 [00:21<00:21, 1.45s/steps, loss=(array(0.07956423, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
53%|█████▎ | 16/30 [00:22<00:18, 1.33s/steps, loss=(array(0.07956423, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
53%|█████▎ | 16/30 [00:22<00:18, 1.33s/steps, loss=(array(0.07881958, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
57%|█████▋ | 17/30 [00:23<00:16, 1.24s/steps, loss=(array(0.07881958, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
57%|█████▋ | 17/30 [00:23<00:16, 1.24s/steps, loss=(array(0.07812418, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
60%|██████ | 18/30 [00:24<00:14, 1.20s/steps, loss=(array(0.07812418, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
60%|██████ | 18/30 [00:25<00:14, 1.20s/steps, loss=(array(0.07755722, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
63%|██████▎ | 19/30 [00:25<00:13, 1.21s/steps, loss=(array(0.07755722, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
63%|██████▎ | 19/30 [00:26<00:13, 1.21s/steps, loss=(array(0.07703114, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
67%|██████▋ | 20/30 [00:27<00:12, 1.25s/steps, loss=(array(0.07703114, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
67%|██████▋ | 20/30 [00:27<00:12, 1.25s/steps, loss=(array(0.07644749, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
70%|███████ | 21/30 [00:28<00:10, 1.15s/steps, loss=(array(0.07644749, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
70%|███████ | 21/30 [00:28<00:10, 1.15s/steps, loss=(array(0.07577264, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
73%|███████▎ | 22/30 [00:29<00:10, 1.30s/steps, loss=(array(0.07577264, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
73%|███████▎ | 22/30 [00:30<00:10, 1.30s/steps, loss=(array(0.07500708, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
77%|███████▋ | 23/30 [00:31<00:09, 1.42s/steps, loss=(array(0.07500708, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
77%|███████▋ | 23/30 [00:32<00:09, 1.42s/steps, loss=(array(0.07421581, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
80%|████████ | 24/30 [00:33<00:09, 1.55s/steps, loss=(array(0.07421581, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
80%|████████ | 24/30 [00:33<00:09, 1.55s/steps, loss=(array(0.07351583, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
83%|████████▎ | 25/30 [00:34<00:07, 1.50s/steps, loss=(array(0.07351583, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
83%|████████▎ | 25/30 [00:35<00:07, 1.50s/steps, loss=(array(0.07295816, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
87%|████████▋ | 26/30 [00:35<00:05, 1.44s/steps, loss=(array(0.07295816, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
87%|████████▋ | 26/30 [00:36<00:05, 1.44s/steps, loss=(array(0.07251285, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
90%|█████████ | 27/30 [00:37<00:04, 1.48s/steps, loss=(array(0.07251285, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
90%|█████████ | 27/30 [00:38<00:04, 1.48s/steps, loss=(array(0.07211037, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
93%|█████████▎| 28/30 [00:38<00:02, 1.41s/steps, loss=(array(0.07211037, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
93%|█████████▎| 28/30 [00:39<00:02, 1.41s/steps, loss=(array(0.07173611, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
97%|█████████▋| 29/30 [00:40<00:01, 1.42s/steps, loss=(array(0.07173611, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:260: UserWarning: Using a target size (torch.Size([1, 1, 1, 256, 256])) that is different to the input size (torch.Size([1, 1, 256, 256])). This will likely lead to incorrect results due to broadcasting. Please ensure they have the same size.
loss = torch.nn.functional.mse_loss(out, image[None, None])
97%|█████████▋| 29/30 [00:40<00:01, 1.42s/steps, loss=(array(0.07137462, dtype=float32),)]/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:276: UserWarning: Ignoring specified arguments in this call because figure with num: 1 already exists
fig, axs = plt.subplots(2, 2, figsize=(10, 10), num=1)
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
100%|██████████| 30/30 [00:41<00:00, 1.38s/steps, loss=(array(0.07137462, dtype=float32),)]
100%|██████████| 30/30 [00:41<00:00, 1.38s/steps, loss=(array(0.07137462, dtype=float32),)]
# Make a GIF of all images.
imgs = [Image.open(img) for img in image_files]
imgs[0].save(
"mrinufft_learn_traj_multires.gif",
save_all=True,
append_images=imgs[1:],
optimize=False,
duration=2,
loop=0,
)
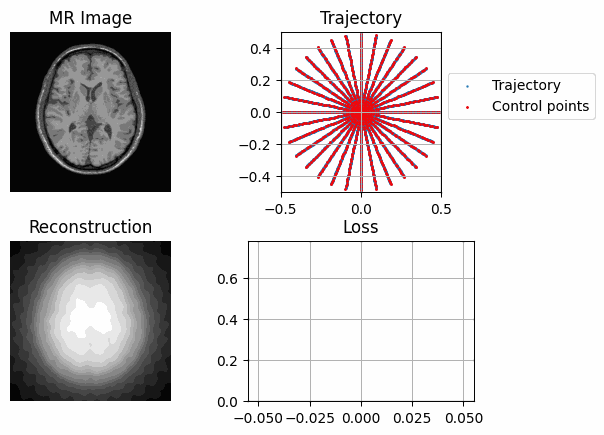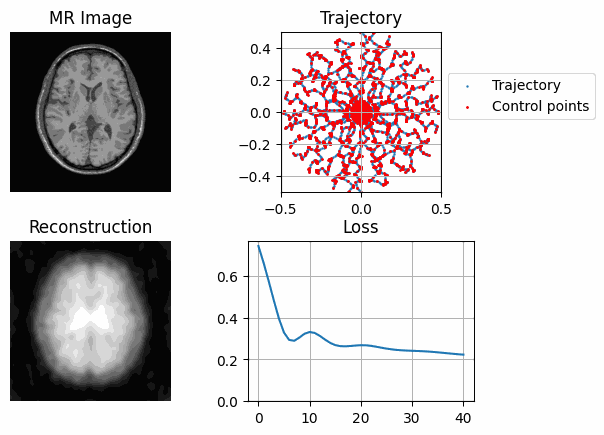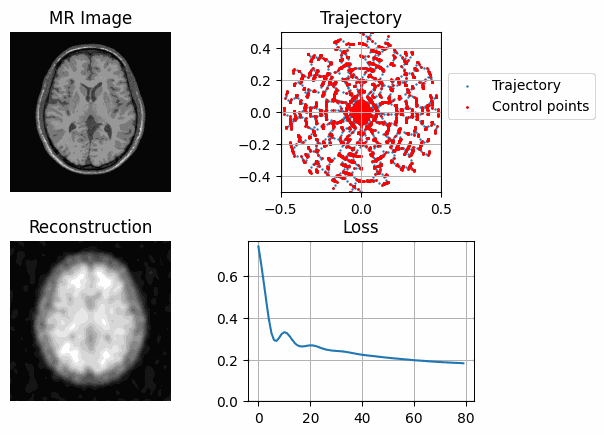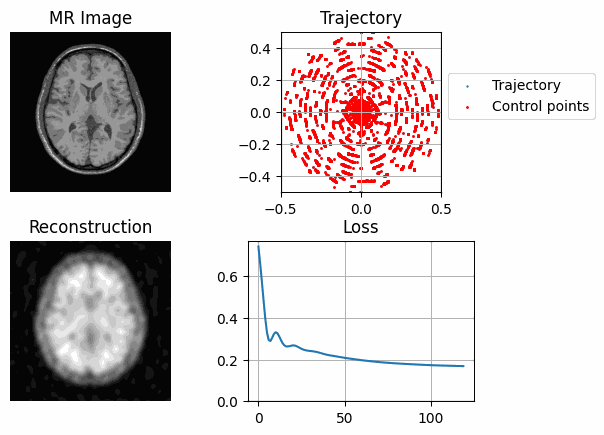
Results#
model.eval()
final_recons = model(image)
final_traj = model.get_trajectory().detach().cpu().numpy()
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:99: UserWarning: Samples will be rescaled to [-0.5, 0.5), assuming they were in [-pi, pi)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/mrinufft/_utils.py:94: UserWarning: Samples will be rescaled to [-pi, pi), assuming they were in [-0.5, 0.5)
warnings.warn(
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/venv/lib/python3.10/site-packages/finufft/_interfaces.py:336: UserWarning: Argument `data` does not satisfy the following requirement: C. Copying array (this may reduce performance)
warnings.warn(f"Argument `{name}` does not satisfy the following requirement: {prop}. Copying array (this may reduce performance)")
fig, axs = plt.subplots(1, 3, figsize=(9, 3))
plot_state(axs, image, final_traj, final_recons)
plt.show()
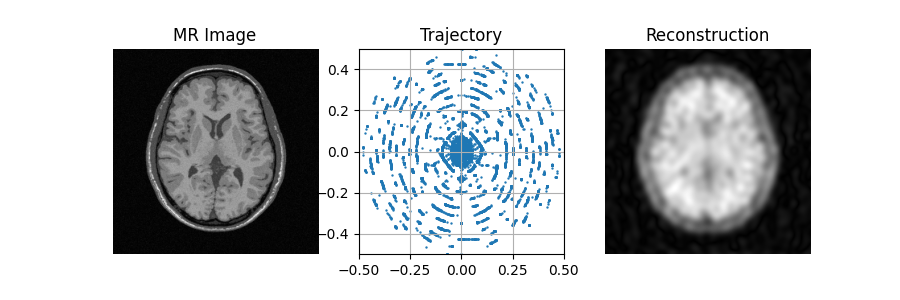
/volatile/github-ci-mind-inria/gpu_runner2/_work/mri-nufft/mri-nufft/examples/example_learn_samples_multires.py:137: DeprecationWarning: __array_wrap__ must accept context and return_scalar arguments (positionally) in the future. (Deprecated NumPy 2.0)
axs[0].imshow(np.abs(image[0]), cmap="gray")
The learned trajectory above improves the reconstruction quality as compared to the initial trajectory shown above. Note of course that the reconstructed image is far from perfect because of the documentation rendering constraints. In order to improve the results one can start by training it for more than just 5 iterations per decimation level. Also density compensation should be used, even though it was avoided here for CPU compliance. Check out Learn Sampling pattern to know more.
References#
N. Chauffert, P. Weiss, J. Kahn and P. Ciuciu, “A Projection Algorithm for Gradient Waveforms Design in Magnetic Resonance Imaging,” in IEEE Transactions on Medical Imaging, vol. 35, no. 9, pp. 2026-2039, Sept. 2016, doi: 10.1109/TMI.2016.2544251.
G. R. Chaithya, P. Weiss, G. Daval-Frérot, A. Massire, A. Vignaud and P. Ciuciu, “Optimizing Full 3D SPARKLING Trajectories for High-Resolution Magnetic Resonance Imaging,” in IEEE Transactions on Medical Imaging, vol. 41, no. 8, pp. 2105-2117, Aug. 2022, doi: 10.1109/TMI.2022.3157269.
Chaithya GR, and Philippe Ciuciu. 2023. “Jointly Learning Non-Cartesian k-Space Trajectories and Reconstruction Networks for 2D and 3D MR Imaging through Projection” Bioengineering 10, no. 2: 158. https://doi.org/10.3390/bioengineering10020158
Total running time of the script: (2 minutes 54.182 seconds)
